Shannon-Fano-Codierung
Du möchtest wissen, was es mit der Shannon-Fano-Codierung auf sich hat? Im folgenden Beitrag erklären wir dir, wie du mithilfe dieser Codierung optimale Codes finden kannst.
Inhaltsübersicht
Shannon-Fano-Kodierung: Entropie
Aber was sind optimale Codes überhaupt? Diese versuchen die mittlere Codewortlänge  zu minimieren. Der minimal erreichbare Idealwert entspricht der Entropie der Quelle, die sich mit
zu minimieren. Der minimal erreichbare Idealwert entspricht der Entropie der Quelle, die sich mit
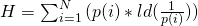
beschreiben lässt. P von i ist dabei die Auftretenswahrscheinlichkeit des Zeichens i, ld der logarithmus dualis und N die Anzahl der Zeichen.
Die Entropie ist in der Informationstheorie ein Maß für den mittleren Informationsgehalt einer Nachricht. Sie beschreibt den durchschnittlichen Informationsgehalt pro Zeichen einer Quelle. Ihre Einheit ist Bit pro Zeichen. Zudem gilt: Je seltener ein Zeichen auftritt, desto höher ist dessen Informationsgehalt.
Durch die Minimierung der mittleren Codewortlänge kommt es zu kürzeren Übertragungszeiten, was wiederum zu höheren Datenraten führt. Das ist super, denn das bedeutet, dass das ein Video jetzt deutlich schneller lädt.
Je länger das Codewort ist, desto länger dauert der Sendevorgang. Wenn nun viele verschiedene Codewörter übertragen werden sollen, dann sollten Ereignisse, die häufiger auftreten, kürzere Codewörter und Ereignisse, die hingegen nur sehr selten vorkommen, längere Codewörter haben. Dadurch kann die mittlere Codewortlänge minimiert werden. Diese lässt sich so berechnen:

Dabei ist  die Auftretenswahrscheinlichkeit und
die Auftretenswahrscheinlichkeit und  die Länge des i-ten Codewortes. n ist die Anzahl der Codewörter. Die mittlere Codewortlänge
die Länge des i-ten Codewortes. n ist die Anzahl der Codewörter. Die mittlere Codewortlänge  kann nie kleiner als die Entropie der Quelle H sein. Bei optimalen Codes ist die mittlere Codewortlänge aber auch nicht sehr viel größer als die Entropie der Sendequelle. Im Idealfall gilt:
kann nie kleiner als die Entropie der Quelle H sein. Bei optimalen Codes ist die mittlere Codewortlänge aber auch nicht sehr viel größer als die Entropie der Sendequelle. Im Idealfall gilt:

Beispiel: Shannon-Fano-Code
Mit der Shannon-Fano-Codierung, die eine Form der Entropiecodierung darstellt, kannst du einen optimalen Code finden. Wie das geht, zeigen wir dir in nur vier Schritten an einem Beispiel. Du willst mit deiner Freundin mal wieder eine gute Bar besuchen. Du hast die Anzahl der bisherigen Besuche in euren Lieblingsbars in einer Strichliste notiert.
Höchstwahrscheinlich geht ihr heute Abend wieder in die Soju Bar, denn an 8 von 34 Abenden wart ihr dort. Daher sollte das Codewort für Soju Bar kurz sein. Dein Ziel ist es also, den Bars möglichst effiziente Codewörter zuzuordnen.
Beginnen wir mit Schritt 1, den Zeichenvorrat linear nach aufsteigender Wahrscheinlichkeit zu sortieren. Zunächst einmal bestimmen wir die relative Häufigkeit der Besuche, damit wir die Bars nach aufsteigender Wahrscheinlichkeit ordnen können. Bei zwei gleich häufigen Ereignissen ist es egal, welches zuerst kommt.
Da die Namen etwas zu lang sind, kürzen wir diese im Folgenden einfach ab, sodass z.B. Barbie Deinhoff’s zu BD und die Weinerei zu DW wird. Nun schreibst du die Abkürzungen nach aufsteigender Wahrscheinlichkeit sortiert auf und versiehst Sie mit der entsprechenden Häufigkeit.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Bildung der Teilmengen
Der erste Schritt ist damit abgehakt. Kommen wir zum zweiten Schritt: Hier gilt es zwei Teilmengen so zu konstruieren, dass die Summenwahrscheinlichkeit der beiden Teilmengen möglichst gleich groß ist.
Da wir jedoch bei den gegebenen Wahrscheinlichkeiten nicht genau die Hälfte 17 von 34 treffen können, halbieren wir zwischen Die Weinerei DW und Luzia L.
Daraufhin folgt auch schon Schritt drei: Hier erhält die erste Teilmenge das Codierungszeichen „0“ und die zweite Teilmenge eine „1“. Jetzt fährst du mit den jeweils gefundenen Teilmengen rekursiv in gleicher Weise fort, bis nur noch ein Zeichen in den resultierenden Teilmengen enthalten ist. Beginnen wir mit der linken Seite, also Teilmenge eins mit 15 von 34. Diese muss jetzt erneut in zwei gleich große Teilmengen separiert werden. Die Hälfte liegt bei 7,5 durch 15, was wir aber auch hier mit den gegebenen Wahrscheinlichkeiten nicht treffen werden. Wir teilen daher zwischen B3 und KAM. Die entstandenen Teilmengen codieren wir wie gehabt mit 0 für die Teilmenge 1 und 1 für die Teilmenge 2.
Nun nehmen wir uns mehrere Farben und teilen die beiden entstandenen Teilmengen erneut. Dabei teilen wir immer näherungsweise in zwei Hälften und kodieren die erste Hälfte mit 0 und die zweite mit 1. Dies führen wir solange fort, bis jede Teilmenge nur noch aus einem Element besteht. Dabei ist es wichtig, die Nullen und Einsen immer sofort aufzuschreiben, damit du den Überblick behältst.
Wie du vielleicht bemerkt hast, ist der Shannon-Fano-Code nicht eindeutig, da es manchmal mehrere Möglichkeiten gibt, zwei annähernd gleich große Teilmengen zu bilden. Dies führt dann zu unterschiedlichen Codewörtern. Beide sind aber richtig, haben also die gleiche mittlere Codewortlänge.
Überprüfung
Nun willst du deinen Code noch überprüfen, ob er wirklich so optimal ist. Dir fällt bestimmt sofort auf, dass seltener besuchte Bars die längeren Codewörter haben. Wir berechnen nun nach unserer Formel die Entropie der Quelle, und die mittlere Codewortlänge des gefundenen Codes.
Zuerst die Entropie: Dazu nehmen wir unsere Formel und formen sie um, sodass der logarithmus dualis aufgelöst wird. Denn so können wir unsere Werte leichter einsetzen.
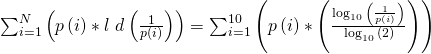
Und genau das machen wir jetzt: Wir setzen die jeweilige Wahrscheinlichkeit der Bar in die Formel ein und bilden daraus die Summe. Das ist eine ziemlich lange Rechnung. Sie folgt jedoch immer dem gleichen Prinzip.

Als Ergebnis erhalten wir: Die Entropie H der Quelle ist gleich 3,0101 bit. Jetzt nehmen wir die Berechnung der mittleren Codewort-Länge in Angriff. Diesmal passt die Formel so, wie sie ist und wir setzen gleich ein: Für p von i ist das die Wahrscheinlichkeit des Besuchs der einzelnen Bars und für m von  die Länge des Codes der Bar.
die Länge des Codes der Bar.
Wenn wir das Ganze dann ausrechnen, erhalten wir eine mittlere Codewortlänge von 3,0588 bit. Der gefundene Code kann also durchaus als optimal bezeichnet werden. Nun bist du also nicht nur perfekt gerüstet, um die Bar per Klopfzeichen zu klären, sondern weißt auch, wie man ganz allgemein Datenübertragung optimieren kann.





