Dynamischer Festigkeitsnachweis
Hallo! Du bist letztens mit deinem Auto auf der Straße liegen geblieben, weil du einen Achsbruch hattest? Wie diese kleine Achse das komplette Gewicht des Autos überhaupt halten kann, erklären wir dir jetzt.
In unserem letzten Video hatten wir das Beispiel der Kleiderstange, bei dem es sich um einen statischen Festigkeitsnachweis gehandelt hat. Bei unserem Auto geht es sich jetzt um den dynamischen Festigkeitsnachweis, da sich die Achse mit dreht und somit die Belastung ständig wechselt, also dynamisch ist. Das Vorgehen ist aber fast dasselbe wie im letzten Video.
Inhaltsübersicht
Wie kann eine Achse das Gewicht eines Autos halten?
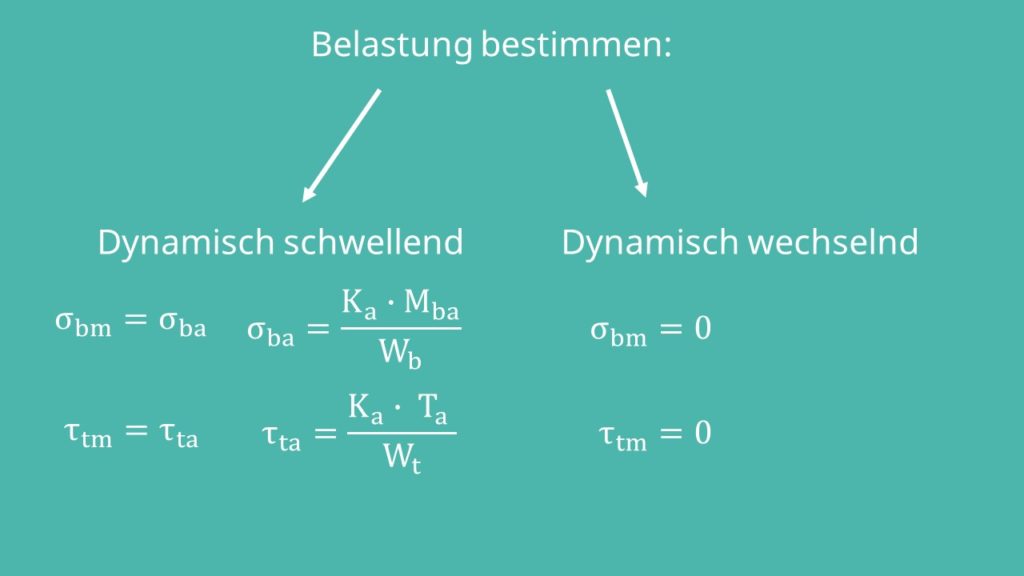
Zuerst einmal musst du wieder deine Belastungen bestimmen und berechnen. Dabei ist es wichtig zu wissen, ob eine dynamisch schwellende oder dynamisch wechselnde Beanspruchungsart vorliegt. Der Unterschied zwischen diesen beiden Beanspruchungsarten macht sich nämlich in der Bestimmung der Mittelspannung bemerkbar. Bei wechselnder Belastung gilt  . Bei schwellender Belastung hingegen gilt:
. Bei schwellender Belastung hingegen gilt:  , wobei
, wobei  die Ausschlagspannung ist. Du berechnest diese mit der Formel
die Ausschlagspannung ist. Du berechnest diese mit der Formel  . Dasselbe gilt auch für die Torsion. Bei wechselnder Belastung ist
. Dasselbe gilt auch für die Torsion. Bei wechselnder Belastung ist  und bei schwellender Belastung
und bei schwellender Belastung  , wobei
, wobei  ist. Dabei ist
ist. Dabei ist  wieder der Anwendungsfaktor, den du aus Tabelle 3-5 bekommst. Für Schweiß-, Niet-, Stift- und Bolzenverbindung also zum Beispiel aus Tabelle 3-5 c.
wieder der Anwendungsfaktor, den du aus Tabelle 3-5 bekommst. Für Schweiß-, Niet-, Stift- und Bolzenverbindung also zum Beispiel aus Tabelle 3-5 c.  beziehungsweise
beziehungsweise  sind die Widerstandsmomente, die je nach Form anders berechnet werden.
sind die Widerstandsmomente, die je nach Form anders berechnet werden.  und
und  sind die Momente, die an deinem Werkstück angreifen.
sind die Momente, die an deinem Werkstück angreifen.
Verschiedene Faktoren zur Berechnung
Dann ist es wichtig den Konstruktionsfaktor  beziehungsweise
beziehungsweise  zu bestimmen, denn dieser berücksichtigt die Bauteilgeometrie. Dafür musst du wiederrum die Kerbformzahl
zu bestimmen, denn dieser berücksichtigt die Bauteilgeometrie. Dafür musst du wiederrum die Kerbformzahl  aus Tabelle 3-6 sowie die Kerbwirkungszahl
aus Tabelle 3-6 sowie die Kerbwirkungszahl  aus Tabelle 3-9 für die Biegung und für die Torsion ablesen. Ebenso brauchst du noch den geometrischen Größeneinflussfaktor
aus Tabelle 3-9 für die Biegung und für die Torsion ablesen. Ebenso brauchst du noch den geometrischen Größeneinflussfaktor  aus Tabelle 3-11c. Den Einflussfaktor
aus Tabelle 3-11c. Den Einflussfaktor  beziehungsweise
beziehungsweise  findest du in Tabelle 3-10. Hier siehst du einen Ausschnitt für Gusswerkstoffe. Zu guter Letzt erhältst du noch den Einflussfaktor der Oberflächenverfestigung
findest du in Tabelle 3-10. Hier siehst du einen Ausschnitt für Gusswerkstoffe. Zu guter Letzt erhältst du noch den Einflussfaktor der Oberflächenverfestigung  aus Tabelle 3-12. So, jetzt kannst du endlich deinen Konstruktionsfaktor für Biegung mit
aus Tabelle 3-12. So, jetzt kannst du endlich deinen Konstruktionsfaktor für Biegung mit  und den für Torsion mit
und den für Torsion mit  berechnen.
berechnen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Wechselfestigkeit der Bauteile
Soweit, so gut. Nun können wir die Wechselfestigkeit der Bauteile bestimmen. Dabei ist die Gestaltwechselfestigkeit für die Biegung  und für die Torsion
und für die Torsion  . Hierfür musst du die Dauerwechselfestigkeitswerte
. Hierfür musst du die Dauerwechselfestigkeitswerte  und
und  aus Tabelle 1-1, sowie den Korrekturfaktor
aus Tabelle 1-1, sowie den Korrekturfaktor  aus Tabelle 3-11 herauslesen.
aus Tabelle 3-11 herauslesen.
Mittelspannungsempfindlichkeit und Vergleichsmittelspannung
Als nächstes fehlen uns noch die Mittelspannungsempfindlichkeit und die Vergleichsmittelspannung. Für die Mittelspannungsempfindlichkeit gilt  und
und  . Die Faktoren zu Berechnung der Mittelempfindlichkeit
. Die Faktoren zu Berechnung der Mittelempfindlichkeit  und
und  kannst du aus Tabelle 3-13 je nach Werkstoff ablesen. Deine Zugfestigkeit
kannst du aus Tabelle 3-13 je nach Werkstoff ablesen. Deine Zugfestigkeit  bekommst du wieder aus Tabelle 1-1. Fehlt nur noch der Faktor zur Berechnung der Schubfestigkeit
bekommst du wieder aus Tabelle 1-1. Fehlt nur noch der Faktor zur Berechnung der Schubfestigkeit 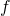 , den du aus Tabelle 3-2 erhältst.
, den du aus Tabelle 3-2 erhältst.
Kommen wir jetzt zur Vergleichsmittelspannung. Für die Normalspannung gilt  . Sie ist also die resultierende Spannung aus Zug-Druck und Biegung. Für die Torsionsspannung haben wir die Formel
. Sie ist also die resultierende Spannung aus Zug-Druck und Biegung. Für die Torsionsspannung haben wir die Formel  .
.
Gestaltausschlagfestigkeit der Bauteile
Jetzt hast du es fast geschafft. Wir brauchen nur noch die Gestaltausschlagfestigkeit der Bauteile. Für die Biegung gilt  und für die Torsion
und für die Torsion  .
.
Wenn dein Bauteil nicht nur auf Biegung und Torsion beansprucht wird, dann kannst du diese Formeln auch für die Berechnung bei einer Zug-Druck und Schub-Beanspruchung verwenden.
Gesamtsicherheit
Jetzt kannst du endlich deine Gesamtsicherheit berechnen. Die Formel dafür lautet  . Nun musst du deine vorhandene berechnete Sicherheit nur noch mit der Mindestsicherheit
. Nun musst du deine vorhandene berechnete Sicherheit nur noch mit der Mindestsicherheit  vergleichen und schon kannst du eine Aussage über die Festigkeit treffen. Wenn
vergleichen und schon kannst du eine Aussage über die Festigkeit treffen. Wenn  ist, dann hält dein Werkstück die Belastung aus. Im anderen Fall, kann es zu Schäden oder sogar zu einem Bruch kommen.
ist, dann hält dein Werkstück die Belastung aus. Im anderen Fall, kann es zu Schäden oder sogar zu einem Bruch kommen.  erhältst du wieder aus Tabelle 3-14.
erhältst du wieder aus Tabelle 3-14.
Endlich geschafft. Wie du siehst ist es gar nicht so schwer die Festigkeit eines Werkstückes bei dynamischer Beanspruchung zu berechnen. Du kannst immer dasselbe Schema verwenden und kommst dann schnell zu einem Ergebnis für die Sicherheit, die das ausschlaggebende Maß zur Beurteilung der Festigkeit eines Bauteils ist.
So, jetzt kannst die Achse deine Autos berechnen und herausfinden, wieso diese gebrochen ist und du liegen geblieben bist. Viel Spaß dabei!