pq Formel einfach erklärt
Du willst wissen, was die pq Formel ist und wie du sie ganz einfach anwendest? Das erfährst du hier!
Inhaltsübersicht
pq Formel einfach erklärt
Mit der pq Formel kannst du quadratische Gleichungen in Normalform lösen. Eine quadratische Gleichung in Normalform kann unterschiedlich aussehen:
| Normalform | Beispiel |
| x2 + px + q = 0 | x2 + 4x + 3 = 0 |
| x2 + px = 0 | x2 + 4x = 0 |
| x2 + q = 0 | x2 + 3 = 0 |
| x2 = 0 |
Hast du eine Gleichung in einer der vier Formen, kannst du die pq Formel anwenden. Sie lautet:
![Rendered by QuickLaTeX.com \[x_{1,2} = -\frac{\textcolor{blue}{p}}{2} \pm \sqrt{\left(\frac{\textcolor{blue}{p}}{2}\right)^2 - \textcolor{orange}{q}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f31bda68a2dce4e166515bb797b243a6_l3.png)
Schau dir gleich an einem Beispiel an, wie du beim Lösen der Gleichung genau vorgehst! Eine Schritt-für-Schritt-Anleitung findest du auch in unserem Video !
Gleichung mit pq Formel lösen
Um mit der pq Formel eine Gleichung zu lösen, gehst du so vor:
- Bringe die Gleichung durch Umformen in Normalform (falls nötig)
- Finde p und q heraus.
- Setze p und q in die pq Formel ein.
- Berechne die beiden Ergebnisse.
- Schreibe die Lösungsmenge auf.
Schau dir die Schritte am Beispiel x2 + 4x + 3 = 0 an.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
1. Gleichung in Normalform bringen
Bei x2 + 4x + 3 = 0 hast du schon eine Normalform. Du kannst Schritt 1 also überspringen.
Anders sieht es bei diesen Beispielen aus:
-
x2 + 4x = –3 → hier musst du zuerst die –3 auf die andere Seite bringen. Rechne dazu auf beiden Seiten +3.

-
2x2 + 4x + 3 = 0 → hier steht eine Zahl vor dem x2. Um eine Normalform zu bekommen, teilst du auf beiden Seiten durch 2.

-
–x2 + 4x + 3 = 0 → hier steht ein Minus vor dem x2. Um eine Normalform zu bekommen, rechnest du auf beiden Seiten mal (-1). Dabei ändern sich einfach alle Vorzeichen — aus jedem Plus wird ein Minus und umgekehrt.

2. p und q herausfinden
p und q herauszufinden ist einfach: p ist die Zahl vor dem x und q ist die Zahl ohne x. Im Beispiel x2 + 4x + 3 = 0 ist also p = 4 und q = 3.
Manchmal fehlt in der Gleichung aber die Zahl vor dem x oder die Zahl ohne x. Dann kannst du einige Merkregeln beachten, um p und q trotzdem zu finden:
- Kein px in der Gleichung → p = 0
Beispiel: x2 + 3 = 0 -
Keine Zahl vor dem x → p = 1
Beispiel: x2 + x + 3 = 0
-
Minus vor dem x → p = -1
Beispiel: x2– x + 3 = 0 - Kein q in der Gleichung → q = 0
Beispiel: x2 + 4x = 0
Übrigens: Ist p oder q in deiner Gleichung 0, kannst du natürlich die pq Formel anwenden. Es gibt in diesen Fällen aber auch leichtere Lösungsverfahren. Schau dir in unserem Video an, wie du dabei vorgehen kannst.
3. p und q in die pq Formel einsetzen
Setze im Beispiel p = 4 und q = 3 in die pq Formel ein:

4. Ergebnisse der pq Formel berechnen
Meistens erhältst du mit der pq Formel zwei Ergebnisse. Für die erste Lösung x1 schreibst du ein Plus vor die Wurzel, für die zweite Lösung x2 ein Minus:
![Rendered by QuickLaTeX.com \[x_{1} = -\frac{\textcolor{blue}{4}}{2} \textcolor{magenta}{+} \sqrt{\left(\frac{\textcolor{blue}{4}}{2}\right)^2 - \textcolor{orange}{3}} = -2 + \sqrt{2^2-3} = -2 + 1 = -1\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-19ae0a4bfa06d05b3a37bc6932b0d11f_l3.png)
![Rendered by QuickLaTeX.com \[x_{2} = -\frac{\textcolor{blue}{4}}{2} \textcolor{magenta}{-} \sqrt{\left(\frac{\textcolor{blue}{4}}{2}\right)^2 - \textcolor{orange}{3}} = -2 - \sqrt{2^2-3} = -2 - 1 = -3\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d081695b0acb7f8f9f6f3301ad4b2547_l3.png)
5. Lösungsmenge aufschreiben
Zum Schluss gibst du noch die Lösungsmenge an. Dafür schreibst du einfach die beiden Lösungen x1 = -1 und x2 = -3 in geschweifte Klammern. Die Lösungsmenge bezeichnest du dann mit dem Buchstaben L:
L = {-1, -3}
Wichtig! Nicht immer gibt es bei der pq Formel zwei Lösungen! Manchmal gibt es auch nur eine Lösung oder überhaupt keine. Schau dir diese Fälle an Beispielen an.
Beispiel 1: pq Formel mit einer Lösung
Löse die quadratische Gleichung x2 – 4x + 4 = 0 mithilfe der pq Formel.
-
Gleichung in Normalenform bringen
Die Gleichung ist schon in Normalform.
-
p und q herausfinden
p = -4 und q = 4
-
p und q in die pq Formel einsetzen

-
Ergebnisse der pq Formel berechnen
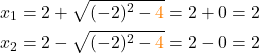
→ Du bekommt hier beides Mal das gleiche Ergebnis. Es gibt also nur eine Lösung, nämlich x = 2.
-
Lösungsmenge aufschreiben
Die Lösungsmenge ist also L = {2}.
Wie kannst du schon vor dem Rechnen herausfinden, ob es nur eine Lösung gibt? Dafür gibt es einen Trick.
Merke: Wenn bei der pq Formel unter der Wurzel eine 0 herauskommt, gibt es nur eine Lösung. Du kannst also einfach vor dem eigentlichen Rechnen den Teil  unter der Wurzel ermitteln. Ergibt das 0, hat die Gleichung nur eine Lösung. Du nennst den Term unter der Wurzel auch Diskriminante
.
unter der Wurzel ermitteln. Ergibt das 0, hat die Gleichung nur eine Lösung. Du nennst den Term unter der Wurzel auch Diskriminante
.
Beispiel 2: pq Formel ohne Lösung
Löse die Gleichung 2x2 – 2x + 4 = 0 nach x auf.
-
Gleichung in Normalenform bringen
Teile alles durch 2, um die Gleichung auf Normalform zu bringen:
-
p und q herausfinden
p = -1 und q = 2
-
p und q in die pq Formel einsetzen

-
Ergebnisse der pq Formel berechnen
![Rendered by QuickLaTeX.com \[x_{1} = \frac{1}{2} + \sqrt{\left(\frac{\textcolor{blue}{-1}}{2}\right)^2 - \textcolor{orange}{2}} = \frac{\textcolor{blue}{1}}{2} + \sqrt{\frac{1}{4} - \textcolor{orange}{2}} = \frac{\textcolor{blue}{1}}{2} + \sqrt{-\frac{7}{4}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-03159a508f99033338b289a91ed2eeeb_l3.png)
![Rendered by QuickLaTeX.com \[x_{2} = \frac{1}{2} - \sqrt{\left(\frac{\textcolor{blue}{-1}}{2}\right)^2 - \textcolor{orange}{2}} = \frac{\textcolor{blue}{1}}{2} - \sqrt{\frac{1}{4} - \textcolor{orange}{2}} = \frac{\textcolor{blue}{1}}{2} - \sqrt{-\frac{7}{4}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c3d98422ecaa12e1299aeaf11b760b30_l3.png)
→ Unter der Wurzel steht eine Minuszahl. Die Wurzel aus negativen Zahlen kannst du aber gar nicht ziehen! Deshalb hat die Gleichung keine Lösung.
-
Lösungsmenge aufschreiben
Die Lösungsmenge ist also L = { }.
Merke: Wenn bei der pq Formel unter der Wurzel eine Minuszahl herauskommt, gibt es keine Lösung.
pq Formel Herleitung
Woher kommen die pq Formeln eigentlich? Das siehst du an der Herleitung der pq Formel. Schau dir dafür zunächst eine allgemeine Gleichung in Normalform an. Du willst sie nach x auflösen. Bringe dazu als Erstes das q auf die andere Seite:
x2 + px + q = 0 | – q
x2 + px = – q
Mache nun eine quadratische Ergänzung
auf der linken Seite. Dazu schreibst du zuerst px als  um. Wozu das gut ist, siehst du später in der Rechnung. Dann addierst du auf beiden Seiten
um. Wozu das gut ist, siehst du später in der Rechnung. Dann addierst du auf beiden Seiten  .
.

Nun kannst du die linke Seite mit der ersten binomischen Formel vereinfachen:
![Rendered by QuickLaTeX.com \[\left(x+\frac{\textcolor{blue}{p}}{2}\right)^2 = \left(\frac{\textcolor{blue}{p}}{2}\right)^2-\textcolor{orange}{q}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1dab45f7d49acb258292df5c86740c36_l3.png)
Im letzten Schritt musst du nur noch die Wurzel ziehen :
![Rendered by QuickLaTeX.com \[x + \frac{\textcolor{blue}{p}}{2} = \pm \sqrt{\left(\frac{\textcolor{blue}{p}}{2}\right)^2-\textcolor{orange}{q}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0e577b2923811f0eb104fa85b43e0964_l3.png)
Wenn du noch  auf die andere Seite bringst, erhältst du als Ergebnis erhältst du die pq Formeln:
auf die andere Seite bringst, erhältst du als Ergebnis erhältst du die pq Formeln:
![Rendered by QuickLaTeX.com \[\Rightarrow x_{1,2} =- \frac{\textcolor{blue}{p}}{2} \pm \sqrt{\left(\frac{\textcolor{blue}{p}}{2}\right)^2-\textcolor{orange}{q}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-7172f92aee553fb3b39636eb2929219c_l3.png)
pq Formel einfach erklärt — häufigste Fragen
(ausklappen)
pq Formel einfach erklärt — häufigste Fragen
(ausklappen)-
Was muss bei einer quadratischen Gleichung stimmen, damit ich die pq-Formel benutzen kann?Du kannst die pq-Formel benutzen, wenn die Gleichung die Form
 hat. Entscheidend ist, dass vor
hat. Entscheidend ist, dass vor  keine Zahl steht, also der Koeffizient 1 ist. Dann liest du p und q ab und setzt beide in die Formel ein.
keine Zahl steht, also der Koeffizient 1 ist. Dann liest du p und q ab und setzt beide in die Formel ein.
-
Wie bringe ich eine Gleichung so in Normalform, dass vor x² wirklich eine 1 steht?Du bringst vor
 eine 1, indem du die ganze Gleichung durch die Zahl vor
eine 1, indem du die ganze Gleichung durch die Zahl vor  teilst. Steht dort ein Minus, kannst du auch mit (–1) multiplizieren, dann wechseln alle Vorzeichen. Beispiel: Aus
teilst. Steht dort ein Minus, kannst du auch mit (–1) multiplizieren, dann wechseln alle Vorzeichen. Beispiel: Aus  wird
wird  .
.
-
Wie lese ich p und q aus der Normalform richtig ab?In der Normalform
 ist p die Zahl vor dem x und q die Zahl ohne x. Achte dabei auf das Vorzeichen, weil es zu p und q dazugehört. Beispiel: Bei
ist p die Zahl vor dem x und q die Zahl ohne x. Achte dabei auf das Vorzeichen, weil es zu p und q dazugehört. Beispiel: Bei  gilt
gilt  und
und  .
.
-
Was setze ich für p ein, wenn vor dem x keine Zahl steht oder nur ein Minus steht?Wenn vor dem x keine Zahl steht, setzt du für p den Wert 1 ein, weil dann
 dasselbe ist wie
dasselbe ist wie  . Steht nur ein Minus vor dem x, setzt du
. Steht nur ein Minus vor dem x, setzt du  ein, weil
ein, weil  dasselbe ist wie
dasselbe ist wie  . Beispiele:
. Beispiele:  hat
hat  ,
,  hat
hat  .
.
-
Wie erkenne ich schon vor dem Ausrechnen, ob es zwei Lösungen, eine Lösung oder keine Lösung gibt?Du erkennst das an dem Term unter der Wurzel
 . Ist er positiv, gibt es zwei Lösungen, bei 0 gibt es genau eine Lösung und bei einer Minuszahl gibt es keine Lösung. Beispiel: Bei
. Ist er positiv, gibt es zwei Lösungen, bei 0 gibt es genau eine Lösung und bei einer Minuszahl gibt es keine Lösung. Beispiel: Bei  wird der Wurzelterm 0, daher ist
wird der Wurzelterm 0, daher ist  die einzige Lösung.
die einzige Lösung.
Mitternachtsformel
Wenn vor dem x2 eine Zahl steht, musst du deine Gleichung nicht unbedingt umformen. Du kannst auch die Mitternachtsformel anwenden. Wie das genau geht, erfährst du hier!
