Wie erkenne ich, ob ich Summenregel oder Produktregel brauche?

Du brauchst die Summenregel bei Plus oder Minus zwischen Termen und die Produktregel bei einer echten Multiplikation. Bei oder leitest du jeden Summanden getrennt ab. Bei musst du beide Faktoren mit Produktregel kombinieren, zum Beispiel bei .

Welche Fehler passieren oft bei Minuszeichen in der Differenzregel?

Ein häufiger Fehler ist, das Minuszeichen beim Ableiten des rechten Terms zu verlieren oder doppelt zu setzen. Bei bleibt das Minus vor stehen, also . Zum Beispiel wird aus korrekt .

Wie leite ich eine Funktion mit drei oder mehr Summanden ab?

Eine Funktion mit drei oder mehr Summanden leitest du ab, indem du jeden Summanden einzeln ableitest und die Ergebnisse wieder mit denselben Vorzeichen zusammensetzt. Das ist die Summen- und Differenzregel mehrfach hintereinander angewendet. Zum Beispiel wird aus die Ableitung .

Wann muss ich beim Ableiten zuerst Klammern ausmultiplizieren?

Du musst Klammern nur dann ausmultiplizieren, wenn in der Klammer nichts multipliziert oder „verkettet“ ist, sondern nur eine Summe steht und es dir das Ableiten erleichtert. Bei ist Ausmultiplizieren optional, weil die Faktorregel reicht. Bei ist Ausmultiplizieren nicht nötig, weil die Produktregel direkt passt.

Warum darf ich die Ableitung nicht über eine Multiplikation verteilen?

Du darfst die Ableitung nicht „verteilen“, weil allgemein gilt. Stattdessen liefert die Produktregel , weil sich bei einer Änderung von beide Faktoren gleichzeitig ändern. Zum Beispiel ist , aber wäre falsch.

Video

Quiz

Summenregel und Differenzregel

Wichtige Inhalte in diesem Video

Summenregel einfach erklärt

(00:12)

Summenregel Beispiele

(00:34)

Differenzregel einfach erklärt

(02:24)

Differenzregel Beispiele

(02:51)

In diesem Artikel erklären wir dir, wie du mit der Summenregel und der Differenzregel Ableitungen bilden kannst. Dabei rechnen wir viele Beispiele.

Du würdest gerne mehr über die Summenregel und Differenzregel lernen? Dann sieh dir unbedingt unser Video dazu an.

Inhaltsübersicht

Summenregel einfach erklärt

im Videozur Stelle im Video springen

(00:12)

Die Summenregel sagt dir, wie du Funktionen mit Summen ableiten kannst.

Summenregel

$f(x)=g(x)+h(x) \quad \rightarrow \quad f'(x)=g'(x) + h'(x)$

Das heißt, um die Summe f(x)=g(x)+h(x) ableiten zu können, musst du zuerst einzeln die Ableitungen g'(x) und h'(x) berechnen. Danach addierst du sie einfach.

Summenregel Beispiele

im Videozur Stelle im Video springen

(00:34)

Es folgen nun einige Beispiele in welchen wir dir zeigen, wie du mit der Summenregel Funktionen ableiten kannst.

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Beispiel 1

Wir wollen die Summe

f(x)= 3x^2+2x

ableiten.

Wie du siehst werden hier zwei Funktionen addiert (+). Das bedeutet wir brauchen die Summenregel. Die Funktion links vom Pluszeichen sei g(x) , die rechts davon h(x) :

$f(x) = \underbrace{3x^2}_{g(x)}+\underbrace{2x}_{h(x)}.$

Nun musst du die Ableitungen g'(x) und h'(x) berechnen. Dafür benötigst du die Potenz- und die Faktorregel . Sie liefern dir:

g'(x)=6x

h'(x)=2.

Als nächstes addierst du deine Ergebnisse und erhältst damit die Ableitung

f'(x)=g'(x)+h'(x)

=6x +2.

Schauen wir uns noch ein weiteres Beispiel an.

Beispiel 2

Gegeben sei die Funktion

$f(x)=4x^5+ x^{-3}$

und du sollst ihre Ableitung berechnen. Da f(x) eine Summe ist, wirst du sie erneut mit der Summenregel ableiten. Hierfür sei g(x)=4x^5 und $h(x)=x^{-3}$ . Du berechnest also zunächst wieder die Ableitungen der einzelnen Funktionen. In diesem Fall erhältst du

g'(x)=20x^4

$h'(x)=-3x^{-4}.$

Anschließend addierst du wieder die Ergebnisse

$f'(x)=20x^4+(-3x^{-4})$

$=20x^4-3x^{-4}.$

Es folgt nun noch ein letztes Beispiel zur Summenregel.

Beispiel 3

Du hast nun die Funktion

$f(x)= -5x^{-3} + 2x^{-4}.$

Für ihre Ableitung verwendest du erneut die Summenregel und bekommst so als Ergebnis:

$f'(x)=15x^{-4} + (-8x^{-5})$

$=15x^{-4}-8x^{-5}.$

Nun weißt du, wie du jede Summe ableiten kannst. Aber wie steht es mit Differenzen?

Differenzregel einfach erklärt

im Videozur Stelle im Video springen

(02:24)

Die Differenzregel sagt dir, wie du Differenzen ableiten kannst.

Differenzregel

$f(x)=g(x)-h(x) \quad \rightarrow \quad f'(x)=g'(x)-h'(x)$

Das heißt, wie bei der Summenregel berechnest du als erstes einzeln die Ableitung der Funktion links und die Ableitung der Funktion rechts vom Minuszeichen. Danach ziehst du sie voneinander ab.

Differenzregel Beispiele

im Videozur Stelle im Video springen

(02:51)

Auch für diese Regel sehen wir uns eine Reihe von Beispielen an.

Beispiel 1

Nun hast du eine Differenz

$f(x)=2x^{2}-x$

gegeben. Um die Ableitung zu bestimmen, gehst du genauso vor, wie bei der Summenregel. Das heißt du identifizierst wieder die Funktionen g(x) und h(x) :

$f(x)=\underbrace{2x^{2}}_{g(x)}-\underbrace{x}_{h(x)}$

und berechnest ihre Ableitungen:

g'(x)=4x

h'(x)=1.

Der Unterschied ist nun, dass du deine Ergebnisse subtrahierst anstatt addierst. Damit erhältst du auch schon die Ableitung

f'(x)=g'(x)-h'(x)

=4x-1.

Beispiel 2

Sieh dir eine weitere Funktion an, nämlich

$f(x)=\underbrace{7x^{2}}_{g(x)}-\underbrace{5x^{-6}}_{h(x)}.$

Da sie eine Differenz ist, berechnest du ihre Ableitung mit der Differenzregel. Das heißt, du bestimmst wieder die Ableitung der Funktion links ( g(x) ), und der Funktion rechts ( h(x) ) vom Minuszeichen. Die Ergebnisse subtrahierst du und erhältst so

f'(x)= g'(x)-h'(x)

$=14x-(-30x^{-7})$

$=14x+30x^{-7}.$

Vermutlich dürfte dir jetzt das Vorgehen klar sein, aber schauen wir uns noch ein letztes Beispiel zur Differenzregel an.

Beispiel 3

Gegeben ist die Differenz

$f(x)=-2x^{-3}-x^{-5}.$

Die Differenzregel liefert dir ihre Ableitung

$f'(x)=6x^{-4}-(-5x^{-6})$

$=6x^{-4}+5x^{-6}.$

Weitere Ableitungsregeln

Neben der Summenregel und der Differenzregel gibt es noch weitere wichtige Ableitungsregeln, die du kennen solltest. Wir haben dir alle in folgender Tabelle zusammengefasst.

Ableitungsregel	Funktion	Ableitung
Produktregel	$f(x)=g(x)\cdot h(x)$	$f'(x)=g'(x)\cdot h(x)+g(x)\cdot h'(x)$
Quotientenregel	$f(x)=\frac{g(x)}{h(x)}$	$f'(x)=\frac{g'(x)\cdot h(x)-g(x)\cdot h'(x)}{[h(x)]^2}$
Kettenregel		$f'(x)=g'(h(x))\cdot h'(x)$
Faktorregel	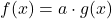$f(x)=a\cdot g(x)$	$f'(x)=a \cdot g'(x)$
Potenzregel		$f'(x)=n\cdot x^{n-1}$
Summenregel
Differenzregel

Summenregel und Differenzregel — häufigste Fragen

(ausklappen)

Wie erkenne ich, ob ich Summenregel oder Produktregel brauche?

Du brauchst die Summenregel bei Plus oder Minus zwischen Termen und die Produktregel bei einer echten Multiplikation. Bei oder leitest du jeden Summanden getrennt ab. Bei $f(x)=g(x)\cdot h(x)$ musst du beide Faktoren mit Produktregel kombinieren, zum Beispiel bei $(x^2+1)\cdot x$ .
Welche Fehler passieren oft bei Minuszeichen in der Differenzregel?

Ein häufiger Fehler ist, das Minuszeichen beim Ableiten des rechten Terms zu verlieren oder doppelt zu setzen. Bei bleibt das Minus vor stehen, also . Zum Beispiel wird aus $7x^2-5x^{-6}$ korrekt $14x-(-30x^{-7})=14x+30x^{-7}$ .
Wie leite ich eine Funktion mit drei oder mehr Summanden ab?

Eine Funktion mit drei oder mehr Summanden leitest du ab, indem du jeden Summanden einzeln ableitest und die Ergebnisse wieder mit denselben Vorzeichen zusammensetzt. Das ist die Summen- und Differenzregel mehrfach hintereinander angewendet. Zum Beispiel wird aus $f(x)=3x^2-2x+x^{-3}$ die Ableitung $f'(x)=6x-2-3x^{-4}$ .
Wann muss ich beim Ableiten zuerst Klammern ausmultiplizieren?

Du musst Klammern nur dann ausmultiplizieren, wenn in der Klammer nichts multipliziert oder „verkettet“ ist, sondern nur eine Summe steht und es dir das Ableiten erleichtert. Bei ist Ausmultiplizieren optional, weil die Faktorregel reicht. Bei $(x^2+1)\cdot(x-3)$ ist Ausmultiplizieren nicht nötig, weil die Produktregel direkt passt.
Warum darf ich die Ableitung nicht über eine Multiplikation verteilen?

Du darfst die Ableitung nicht „verteilen“, weil allgemein $(g(x)\cdot h(x))' \neq g'(x)\cdot h'(x)$ gilt. Stattdessen liefert die Produktregel $(g\cdot h)'=g'\cdot h+g\cdot h'$ , weil sich bei einer Änderung von beide Faktoren gleichzeitig ändern. Zum Beispiel ist $(x\cdot x)'=2x$ , aber $x'\cdot x'=1\cdot1=1$ wäre falsch.

Herleitung Summenregel

Im Folgenden wollen wir die Summenregel einmal herleiten. Dafür stellst du die Ableitung der Funktion

f(x)=g(x)+h(x)

als Differentialquotient mit der h-Methode dar:

$f'(x)=\lim \limits_{h\to 0} \frac{f(x+h)-f(x)}{h}$

$= \lim \limits_{h\to 0} \frac{g(x+h)+h(x+h)-(g(x)+h(x))}{h}.$

Im nächsten Schritt löst du die Klammer im Zähler auf. Dabei ändern sich die Vorzeichen der Funktionen g(x) und h(x) :

$f'(x)= \lim \limits_{h\to 0} \frac{g(x+h)+h(x+h)-g(x)-h(x)}{h}.$

Ist das getan, kannst du das Kommutativgesetz anwenden und die Funktionen g(x) und h(x+h) samt Vorzeichen vertauschen:

$f'(x)= \lim \limits_{h\to 0} \frac{g(x+h)-g(x)+h(x+h)-h(x)}{h}.$

Danach spaltest du den Bruch in zwei Brüche auf:

$f'(x)= \lim \limits_{h\to 0} \left(\frac{g(x+h)-g(x)}{h}+\frac{h(x+h)-h(x)}{h}\right)$

und betrachtest nun zwei separate Grenzwerte:

$f'(x)= \lim \limits_{h\to 0} \frac{g(x+h)-g(x)}{h}+\lim \limits_{h\to 0} \frac{h(x+h)-h(x)}{h}.$

Siehst du dir jetzt nochmal die Formel für den Differentialquotient an, erkennst du, dass die zwei Grenzwerte den Ableitungen g'(x) und h'(x) entsprechen:

f'(x)=g'(x)+ h'(x).