Gewinnfunktion und Erlösfunktion
In diesem Artikel werden wir dir den Zusammenhang zwischen der Gewinn- und der Erlösfunktion näherbringen. Du erfährst unter anderem, wie du die Gewinnfunktion aufstellst und findest wichtige Infos zur Erlösfunktion.
Mit unserem Video erfährst du all das in wenigen Minuten! Außerdem hast du zu diesem Thema die Möglichkeit dein Wissen mit unserer Übungsaufgabe , den Verständnisfragen und einer Klausuraufgabe zu testen.
Inhaltsübersicht
Gewinnfunktion
Als Gewinnfunktion wird die Differenz zwischen der Erlösfunktion und der Kostenfunktion bezeichnet. Sie gibt an, wie viel Gewinn ein Unternehmen durch seine verkauften Produkte realisiert.
Die Gewinnfunktion wird durch  dargestellt. Einfach ausgedrückt ermittelt sie den positiven oder negativen Überschuss, der nach Einnahmen minus Ausgaben übrigbleibt. Für das Ergebnis der Kostenfunktion ergeben sich drei verschiedene Möglichkeiten: Gewinn, Verlust oder der Break-even-point
. Unternehmen können mithilfe der Gewinnfunktion ihre optimale Ausbringungsmenge , die zum maximalen Gewinn führt, bestimmen, indem sie von der Erlösfunktion die Kostenfunktion abziehen.
dargestellt. Einfach ausgedrückt ermittelt sie den positiven oder negativen Überschuss, der nach Einnahmen minus Ausgaben übrigbleibt. Für das Ergebnis der Kostenfunktion ergeben sich drei verschiedene Möglichkeiten: Gewinn, Verlust oder der Break-even-point
. Unternehmen können mithilfe der Gewinnfunktion ihre optimale Ausbringungsmenge , die zum maximalen Gewinn führt, bestimmen, indem sie von der Erlösfunktion die Kostenfunktion abziehen.
Unter einer Erlösfunktion versteht man den Umsatz, der durch die verkauften Produkte eines Unternehmens generiert wird. Sie wird durch angegeben und setzt sich aus dem Produkt zwischen Verkaufspreis und Absatzmenge zusammen.

Die Kostenfunktion gibt den Zusammenhang zwischen der Ausbringungsmenge und den daraus anfallenden Kosten an. Die Funktion fügt sich aus fixen und variablen Kosten zusammen.

Gewinnfunktion Formel
Die Gewinnfunktion stellt die Differenz zwischen Erlösfunktion und Kostenfunktion dar.

Hierbei existieren für die Werte, die  annehmen kann, die folgenden drei Möglichkeiten:
annehmen kann, die folgenden drei Möglichkeiten:
-
 ist größer als 0, also positiv: Es wird ein Gewinn erzielt.
ist größer als 0, also positiv: Es wird ein Gewinn erzielt. -
 ist kleiner als 0, also negativ: Es liegt ein Verlust vor.
ist kleiner als 0, also negativ: Es liegt ein Verlust vor. -
 ist gleich 0: Das Unternehmen erreicht den Break-even-point (BEP) oder auch Gewinnschwelle genannt. Hier ist der Fall, dass Erlös und Kosten gleich hoch sind und weder ein Gewinn noch ein Verlust gegeben sind.
ist gleich 0: Das Unternehmen erreicht den Break-even-point (BEP) oder auch Gewinnschwelle genannt. Hier ist der Fall, dass Erlös und Kosten gleich hoch sind und weder ein Gewinn noch ein Verlust gegeben sind.
Gewinnfunktion berechnen
Möchte ein Unternehmen seine optimale Ausbringungsmenge  bestimmen, muss es die erste Ableitung der Gewinnfunktion bilden. Anschließend setzt man die Ableitung mit 0 gleich und löst die Gleichung nach der optimalen Ausbringungsmenge
bestimmen, muss es die erste Ableitung der Gewinnfunktion bilden. Anschließend setzt man die Ableitung mit 0 gleich und löst die Gleichung nach der optimalen Ausbringungsmenge  auf. Wird dieses
auf. Wird dieses  schlussendlich wieder in die Gewinnfunktion eingesetzt, ergibt sich daraus der maximal realisierbare Gewinn des Unternehmens.
schlussendlich wieder in die Gewinnfunktion eingesetzt, ergibt sich daraus der maximal realisierbare Gewinn des Unternehmens.
Betrachten wir als Beispiel eine Michelin-Pommesbude. Diese serviert exklusive Pommeskreationen mit Trüffelmayonnaise und echtem Goldstaub und möchte nun die optimale Ausbringungsmenge anhand der Gewinnfunktion berechnen.
Wir nehmen an, dass die folgende Gewinnfunktion ermittelt wurde. Diese ergibt sich, wie bereits erklärt, aus der Differenz zwischen der Erlösfunktion und der Kostenfunktion:
![Rendered by QuickLaTeX.com G\left(x\right)=[-0,5x^2+1.000x]-[x+199.000]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2698131180400ce85da24ce967b03489_l3.png)
Zunächst bildet die Besitzerin der Pommesbude die erste Ableitung der Gewinnfunktion:
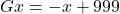
Anschließend setzt sie diese Ableitung mit 0 gleich und löst nach der optimalen Ausbringungsmenge  auf.
auf.


Um nun den maximalen Gewinn zu erhalten, setzt sie die optimale Menge von 999 in ihre ursprünglich bestimmte Gewinnfunktion ein.
![Rendered by QuickLaTeX.com G\left(999\right)=\left[-0,5\cdot{999}^2+1.000\cdot999\right]-\left[999+199.000\right]=300.000,50](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-152305271d2588190c1d208e5a2be94e_l3.png)
Bei der vorliegenden Gewinnfunktion würde die Besitzerin der Pommesbude also mit einer Menge von 999 Portionen das Gewinnmaximum von 300.000,50 € erzielen.
Erlösfunktion
Die Erlösfunktion (oder auch seltener Ertragsfunktion oder Umsatzfunktion) gibt den Gesamtumsatz an, der durch ein verkauftes Produkt generiert wird. Man kann die Erlösfunktion aufstellen, indem das Produkt aus der Preis-Absatz-Funktion (PAF)
 und der Absatzmenge berechnet wird.
und der Absatzmenge berechnet wird.
Die Erlösfunktion gibt also den Zusammenhang zwischen dem Stückpreis und der verkauften Menge eines Gutes wieder.

Nehmen wir an, die Besitzerin der Pommesbude hat die folgende Preis-Absatz-Funktion vorliegen:

Multipliziert sie diese mit der Absatzmenge  , kann sie die Erlösfunktion bestimmen.
, kann sie die Erlösfunktion bestimmen.


Nun möchte die Besitzerin den Erlös, den sie mit ihrer optimalen Ausbringungsmenge von 999 Portionen realisieren kann, berechnen.

Bei 999 verkauften Portionen ihrer Trüffelpommes mit Goldstaub kann sie folglich einen Umsatz von 499.999,50 € erzielen. Mit dem Ergebnis dieser Erlösfunktion kann sie nun durch das Abziehen der Kostenfunktion ihre Gewinnfunktion aufstellen.
Übungsaufgabe
Wenn du denkst, dass du die Theorie nun beherrschst, kannst du die gleich an eine Übungsaufgabe wagen.
Verständnisfragen
Damit du das Thema noch besser verstehst, haben wir einige Fragen für dich zusammengestellt. Dadurch kannst du dein Verständnis noch weiter vertiefen.
Klausuraufgabe
Um zu überprüfen, ob du schon bereit für die Klausur bist, kannst du dich an einer unserer Klausuraufgaben probieren.
Zusammenfassung
Wir fassen noch einmal alle wichtigen Informationen zusammen. Wir haben uns in diesem Artikel mit der Gewinn-, Erlös- und Kostenfunktion auseinandergesetzt. Die Gewinnfunktion ist die Differenz zwischen der Erlösfunktion und der Kostenfunktion. Sie drückt aus, wie viel Gewinn oder Verlust ein Unternehmen unterm Strich generiert. Mithilfe der Gewinnfunktion kann ein Unternehmen die optimale Ausbringungsmenge  bestimmen, die zu seinem maximalen Gewinn führt.
bestimmen, die zu seinem maximalen Gewinn führt.
Die Erlösfunktion gibt den Umsatz an, den ein Unternehmen durch sein verkauftes Produkt erhält. Sie setzt sich aus dem Verkaufspreis multipliziert mit der der Absatzmenge zusammen.
Die Kostenfunktion stellt dar, welche Kosten aufgrund einer Ausbringungsmenge anfallen. Diese erhält man, in dem fixe und variable Kosten aufsummiert werden.
Spätestens jetzt bist du bereit für unsere Übungsaufgabe , die Verständnisfragen und die Klausuraufgabe. Viel Erfolg!





