Video

Quiz

Hier geht's zum Video „Skalarprodukt“

Hier geht's zum Video „Kreuzprodukt / Vektorprodukt“

Vektorrechnung

Wichtige Inhalte in diesem Video

Vektorrechnung Addition

Vektorrechnung Multiplikation

Du möchtest die Vektorrechnung in ihren Grundlagen verstehen und einige Aufgaben dazu rechnen? Dann übe am besten mit diesem Artikel und dem entsprechenden Video einige Rechnungen mit Vektoren.

Inhaltsübersicht

Vektorrechnung einfach erklärt

Erinnere dich kurz, was Vektoren sind:

Vektoren Grundlagen

Ein Vektor ist eine Menge von Pfeilen, die

zueinander parallel sind,
in dieselbe Richtung zeigen (dieselbe Orientierung besitzen) und
gleich lang sind.

Die Länge eines solchen Pfeils nennst du den Betrag | $\vec{x}$ |des Vektors $\vec{x}$ . Du berechnest ihn so:

$|\vec{x}| = \left| \begin{pmatrix} \textcolor{red}{1} \\ \textcolor{blue}{2} \\ \textcolor{olive}{3} \end{pmatrix} \right| = \sqrt{\textcolor{red}{1}^2 + \textcolor{blue}{2}^2 + \textcolor{olive}{3}^2} = \sqrt{1 + 4 + 9} = \sqrt{14} \approx 3.74$

Du kannst Vektoren addieren.

$\textcolor{red}{\begin{pmatrix} 1 \\ 3 \\ 6 \end{pmatrix}} + \textcolor{blue}{\begin{pmatrix} 2 \\ 4 \\ 5 \end{pmatrix}} = \begin{pmatrix} \textcolor{red}{1} + \textcolor{blue}{2} \\ \textcolor{red}{3} + \textcolor{blue}{4} \\ \textcolor{red}{6} + \textcolor{blue}{5} \end{pmatrix} = \begin{pmatrix} 3 \\ 7 \\ 11 \end{pmatrix}$

Du kannst sie mit einer Zahl multiplizieren.

$\textcolor{red}{4} \cdot \textcolor{blue}{\begin{pmatrix} 2 \\ 0 \\ 5 \end{pmatrix}} = \begin{pmatrix} \textcolor{red}{4} \cdot \textcolor{blue}{2} \\ \textcolor{red}{4} \cdot \textcolor{blue}{0} \\ \textcolor{red}{4} \cdot \textcolor{blue}{5} \end{pmatrix} = \begin{pmatrix} 8 \\ 0 \\ 20 \end{pmatrix}$

Aber du kannst auch das Skalarprodukt

$\textcolor{red}{\begin{pmatrix} 1 \\ 8 \\ 7 \end{pmatrix}} \circ \textcolor{blue}{\begin{pmatrix} 2 \\ 5 \\ 6 \end{pmatrix}} = \textcolor{red}{1} \cdot \textcolor{blue}{2} + \textcolor{red}{8} \cdot \textcolor{blue}{5} + \textcolor{red}{7} \cdot \textcolor{blue}{6} = 2 + 40 + 42 = 84$

oder das Kreuzprodukt berechnen.

$\textcolor{red}{\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}} \times \textcolor{blue}{\begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix}} = \begin{pmatrix} \textcolor{red}{2} \cdot \textcolor{blue}{6} - \textcolor{red}{3} \cdot \textcolor{blue}{5} \\ \textcolor{red}{3} \cdot \textcolor{blue}{4} - \textcolor{red}{1} \cdot \textcolor{blue}{6} \\ \textcolor{red}{1} \cdot \textcolor{blue}{5} - \textcolor{red}{2} \cdot \textcolor{blue}{4} \end{pmatrix} = \begin{pmatrix} 12 - 15 \\ 12 - 6 \\ 5 - 8 \end{pmatrix} = \begin{pmatrix} -3 \\ 6 \\ -3 \end{pmatrix}$

Vektorrechnung Addition

im Videozur Stelle im Video springen

Bei der Vektoraddition addierst du zeilenweise die Einträge der Vektoren miteinander.

$\textcolor{red}{\begin{pmatrix} 1 \\ 3 \\ 6 \end{pmatrix}} + \textcolor{blue}{\begin{pmatrix} 2 \\ 4 \\ 5 \end{pmatrix}} = \begin{pmatrix} \textcolor{red}{1} + \textcolor{blue}{2} \\ \textcolor{red}{3} + \textcolor{blue}{4} \\ \textcolor{red}{6} + \textcolor{blue}{5} \end{pmatrix} = \begin{pmatrix} 3 \\ 7 \\ 11 \end{pmatrix}$

Vektoraddition geometrisch

Geometrisch kannst du dir die Addition in der Vektorenrechnung so vorstellen, dass du den Anfang eines Vektors an das Ende (die Spitze) des anderen Vektors klebst.
Das Ergebnis von $\vec{a} + \vec{b}$ ist dann der direkte Weg zwischen dem Schaft von $\vec{a}$ und der Spitze von $\vec{b}$ .

Vektorrechnung, Addition, Vektoraddition, Vektoraddition geometrisch — Vektoraddition geometrisch

Du kannst mit der Subtraktion von zwei Punkten A und B den Vektor ausrechnen, der A und B verbindet. Das ist der Verbindungsvektor $\overrightarrow{AB}$ .

$\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A}$

Also ist der Verbindungsvektor zwischen A = (2 | 8 | 5) und B = (1 | 4 | 3):

$\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} \begin{pmatrix} 1 \\ 4 \\ 3 \end{pmatrix} - \begin{pmatrix} 2 \\ 8 \\ 5 \end{pmatrix} = \begin{pmatrix} 1 - 2 \\ 4 - 8 \\ 3 - 5 \end{pmatrix} = \begin{pmatrix} -1 \\ -4 \\ -2 \end{pmatrix}$

Der Abstand zwischen A und B ist die Länge des Verbindungsvektors $\overrightarrow{AB}$ .

In unserem Beispiel ist der Abstand zwischen A und B also:

$|\overrightarrow{AB}| = \left| \begin{pmatrix} -1 \\ 4 \\ 2 \end{pmatrix} \right| = \sqrt{(-1)^2 + (-4)^2 + (-2)^2} = \sqrt{1 + 16 + 4} = \sqrt{21}$

Vektorrechnung Addition Aufgaben:

Berechne:
$\begin{pmatrix}2 \\5 \\7\end{pmatrix}+\begin{pmatrix}1 \\6 \\3\end{pmatrix}$
Berechne den Abstand der beiden Punkte A(4|2|0) und B(0|8|1).
Du bedienst eine ferngesteuerte Drohne. Du lässt sie zuerst 30m nach oben fliegen. Dann 10m nach rechts. 2m nach unten. 7m nach links. 8m nach vorne. Und wieder 2m nach oben. Wie weit ist die Drohne von ihrem Startpunkt entfernt? (fortgeschritten)

Vektorrechnung Addition Lösungen:

Komponentenweise Addieren ergibt:
$\begin{pmatrix}2 \\5 \\7\end{pmatrix}+\begin{pmatrix}1 \\6 \\3\end{pmatrix}=\begin{pmatrix}2 + 1\\5 + 6\\7 + 3\end{pmatrix}=\begin{pmatrix}3 \\11 \\10\end{pmatrix}$
Der Abstand zwischen zwei Punkten ist die Länge des Verbindungsvektors. Berechne also als erstes den Verbindungsvektor zwischen A und B:
$\overrightarrow{AB} = \vec{B} - \vec{A} = \begin{pmatrix}0 \\8 \\1\end{pmatrix}-\begin{pmatrix}4 \\2 \\0\end{pmatrix}=\begin{pmatrix}-4\\6\\1\end{pmatrix}$

Als nächstes berechnest du die Länge von $\overrightarrow{AB}$ :
$|\overrightarrow{AB}| = \left| \begin{pmatrix} -4 \\ 6 \\ 1 \end{pmatrix} \right| = \sqrt{(-4)^2 + 6^2 + 1^2} = \sqrt{16 + 36 + 1} = \sqrt{53}$

Also beträgt der Abstand zwischen A und B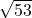 $\sqrt{53}$ , also ungefähr 7,28.
Du kannst jede Bewegung der Drohne als Vektor darstellen. Lege den Startpunkt als (0|0|0) fest und du kannst die aktuelle Position ausrechnen. Addiere dafür die Bewegungsvektoren deiner Drohne. Im klassischen Koordinatensystem entspricht eine Bewegung nach oben einer Bewegung in x3-Richtung. Nach rechts in x2-Richtung und nach hinten in x1-Richtung. Die aktuelle Position kannst du also mit der folgenden Vektoraddition berechnen:

$\begin{pmatrix}0 \\0 \\30\end{pmatrix}+\begin{pmatrix}0 \\10 \\0 \end{pmatrix}+\begin{pmatrix}0 \\0 \\-2\end{pmatrix}+\begin{pmatrix}0 \\-7 \\0 \end{pmatrix}+\begin{pmatrix}-8 \\0 \\0\end{pmatrix}+\begin{pmatrix}0 \\0 \\2\end{pmatrix}=\begin{pmatrix}-8 \\10 - 7 \\30 - 2 + 2\end{pmatrix}=\begin{pmatrix}-8 \\3 \\30\end{pmatrix}$

Das ist der Ortsvektor der Drohne. Ihren Abstand zum Startpunkt (0|0|0) erhältst du, indem du die Länge des Ortsvektors berechnest.
$\left| \begin{pmatrix} -8 \\ 3 \\ 30 \end{pmatrix} \right| = \sqrt{(-8)^2 +3^2 + 30^2} = \sqrt{64 + 9 + 900} = \sqrt{975}$

Die Drohne ist also $\sqrt{975}$ Meter, also ungefähr 31,22 Meter vom Startpunkt entfernt.

Vektorrechnung Multiplikation

im Videozur Stelle im Video springen

Du kannst einen Vektor auch mit einer reellen Zahl r multiplizieren. Du nennst r in diesem Fall ein Skalar. Deshalb heißt die Rechenart auch skalare Multiplikation.
Das Ergebnis erhältst du, indem du jeden Eintrag des Vektors mit r multiplizierst.

$\textcolor{red}{r} \cdot \textcolor{blue}{\begin{pmatrix} 2 \\ 0 \\ 5 \end{pmatrix}} = \begin{pmatrix} \textcolor{red}{r} \cdot \textcolor{blue}{2} \\ \textcolor{red}{r} \cdot \textcolor{blue}{0} \\ \textcolor{red}{r} \cdot \textcolor{blue}{5} \end{pmatrix}$

Vektormultiplikation geometrisch

Geometrisch wird dabei der Vektor um den Faktor r verlängert. Der Vektor $2\vec{a}$ zeigt also in die gleiche Richtung wie $\vec{a}$ , ist aber doppelt so lang. Der Vektor $-2\vec{a}$ ist genauso lang wie $2\vec{a}$ , aber zeigt in die entgegengesetzte Richtung.

Vektorrechnung, Multiplikation, Skalarmultiplikation, skalare Multiplikation — Vektormultiplikation – geometrisch

Vektorrechnung Multiplikation Aufgaben:

Berechne:
$6 \cdot \begin{pmatrix}9 \\8 \\7\end{pmatrix}$
Berechne:
$2 \cdot \begin{pmatrix}4 \\6 \\8\end{pmatrix}$
Welcher Vektor hat die gleiche Länge wie $\vec{a}$ und zeigt in die entgegengesetzte Richtung?

Vektorrechnung Multiplikation Lösungen:

$6 \cdot \begin{pmatrix}9 \\8 \\7\end{pmatrix} = \begin{pmatrix}6 \cdot 9 \\6 \cdot 8 \\6 \cdot 7\end{pmatrix} =\begin{pmatrix}54 \\48 \\42\end{pmatrix}$
$2 \cdot \begin{pmatrix}4 \\6 \\8\end{pmatrix} = \begin{pmatrix}2 \cdot 4 \\2 \cdot 6 \\2 \cdot 8\end{pmatrix} =\begin{pmatrix}8 \\12 \\16\end{pmatrix}$
1. $-\vec{a}$

Skalarprodukt

im Videozur Stelle im Video springen

Das Skalarprodukt ist trotz des ähnlichen Namens etwas anderes als die Skalarmultiplikation.

$\textcolor{red}{\vec{a}} \circ \textcolor{blue}{\vec{b}} = \textcolor{red}{\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}} \circ \textcolor{blue}{\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix}} = \textcolor{red}{a_1} \cdot \textcolor{blue}{b_1} + \textcolor{red}{a_2} \cdot \textcolor{blue}{b_2} + \textcolor{red}{a_3} \cdot \textcolor{blue}{b_3}$

Beim Skalarprodukt multiplizierst du den ersten Eintrag von $\vec{a}$ mit dem ersten Eintrag von $\vec{b}$ , den zweiten Eintrag von $\vec{a}$ mit dem zweiten Eintrag von $\vec{b}$ und den dritten Eintrag von $\vec{a}$ mit dem dritten Eintrag von $\vec{b}$ . Die Ergebnisse dieser drei Multiplikationen addierst du dann und erhältst das Ergebnis.

Am besten lernst du das an einem konkreten Beispiel:

$\textcolor{red}{\begin{pmatrix} 1 \\ 8 \\ 7 \end{pmatrix}} \circ \textcolor{blue}{\begin{pmatrix} 2 \\ 5 \\ 6 \end{pmatrix}} = \textcolor{red}{1} \cdot \textcolor{blue}{2} + \textcolor{red}{8} \cdot \textcolor{blue}{5} + \textcolor{red}{7} \cdot \textcolor{blue}{6} = 2 + 40 + 42 = 84$

Skalarprodukt geometrisch

Geometrisch verrät dir das Skalarprodukt, ob zwei Vektoren im rechten Winkel zueinander stehen oder nicht: Zwei Vektoren stehen genau dann im rechten Winkel zueinander, wenn sie das Skalarprodukt 0 haben. Beachte aber, dass dabei keiner der beiden Vektoren der Nullvektor sein darf.

Beispiel:

$\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \circ \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = 1 \cdot 0 + 0 \cdot 0 + 0 \cdot 1 = 0$

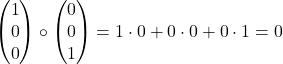
Die beiden Vektoren stehen also im rechten Winkel aufeinander.

Skalarprodukt Aufgaben:

Stehen die beiden Vektoren $\vec{a}$ und $\vec{b}$ senkrecht aufeinander?

$\vec{a} =\begin{pmatrix}2 \\2 \\3\end{pmatrix}\;\vec{b} = \begin{pmatrix}5 \\4 \\-6\end{pmatrix}$
$\vec{a} = \begin{pmatrix}1 \\2 \\3\end{pmatrix}\;\vec{b} = \begin{pmatrix}4 \\5 \\6\end{pmatrix}$

Skalarprodukt Lösungen:

$\vec{a} \circ \vec{b} =\begin{pmatrix}2 \\2 \\3\end{pmatrix}\circ\begin{pmatrix}5 \\4 \\-6\end{pmatrix}= 2 \cdot 5 + 2 \cdot 4 + 3 \cdot (-6) = 10 + 8 - 18 = 0$

Da das Skalarprodukt der beiden Vektoren 0 und Vektor der Nullvektor ist, stehen sie im rechten Winkel zueinander.
$\vec{a} \circ \vec{b} =\begin{pmatrix}1 \\2 \\3\end{pmatrix}\circ\begin{pmatrix}4 \\5 \\6\end{pmatrix}= 1 \cdot 4 + 2 \cdot 5 + 3 \cdot 6 = 4 + 10 + 18 = 32$

Da das Skalarprodukt der beiden Vektoren nicht 0 ist, stehen sie nicht im rechten Winkel zueinander.

Kreuzprodukt

im Videozur Stelle im Video springen

Die letzte Art von Vektorrechnungen ist das Kreuzprodukt , auch oft Vektorprodukt genannt, weil man zwei Vektoren $\vec{a}$ und $\vec{b}$ multipliziert und einen Vektor als Ergebnis erhält. Dieser Vektor steht dann übrigens immer senkrecht auf $\vec{a}$ und $\vec{b}$ .
Das Kreuzprodukt berechnest du so:

$\textcolor{red}{\vec{a}} \times \textcolor{blue}{\vec{b}} = \textcolor{red}{\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}} \times \textcolor{blue}{\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix}} = \begin{pmatrix} \textcolor{red}{a_2} \cdot \textcolor{blue}{b_3} - \textcolor{red}{a_3} \cdot \textcolor{blue}{b_2} \\ \textcolor{red}{a_3} \cdot \textcolor{blue}{b_1} - \textcolor{red}{a_1} \cdot \textcolor{blue}{b_3} \\ \textcolor{red}{a_1} \cdot \textcolor{blue}{b_2} - \textcolor{red}{a_2} \cdot \textcolor{blue}{b_1} \end{pmatrix}$

Ein konkretes Beispiel mit Zahlen rechnest du also so aus:

$\textcolor{red}{\begin{pmatrix} 1 \\ 8 \\ 7 \end{pmatrix}} \times \textcolor{blue}{\begin{pmatrix} 2 \\ 5 \\ 6 \end{pmatrix}} = \begin{pmatrix} \textcolor{red}{8} \cdot \textcolor{blue}{6} - \textcolor{red}{7} \cdot \textcolor{blue}{5} \\ \textcolor{red}{7} \cdot \textcolor{blue}{2} - \textcolor{red}{1} \cdot \textcolor{blue}{6} \\ \textcolor{red}{1} \cdot \textcolor{blue}{5} - \textcolor{red}{8} \cdot \textcolor{blue}{2} \end{pmatrix} = \begin{pmatrix} 48 - 35 \\ 14 - 6 \\ 5 - 16 \end{pmatrix} = \begin{pmatrix} 13 \\ 8 \\ -11 \end{pmatrix}$

Du siehst, dass es eine etwas längere Rechnung ist. Deshalb sind zwei Tipps von uns:

Schreibe den gesamten Rechenweg auf; so wie er hier steht.
Übe das Kreuzprodukt, damit du den Ablauf kannst.

Kreuzprodukt Aufgaben:

Finde einen Vektor, der senkrecht auf den beiden Vektoren $\vec{a}$ und $\vec{b}$ steht mit:

$\vec{a} = \begin{pmatrix}6 \\5 \\4\end{pmatrix}\;\vec{b} = \begin{pmatrix}3 \\2 \\1\end{pmatrix}$
$\vec{a} = \begin{pmatrix}1 \\0 \\0\end{pmatrix}\;\vec{b} = \begin{pmatrix}0 \\1 \\0\end{pmatrix}$

Kreuzprodukt Lösungen:

$\vec{a} \times \vec{b} =\begin{pmatrix}6 \\5 \\4\end{pmatrix}\times\begin{pmatrix}3 \\2 \\1\end{pmatrix}=\begin{pmatrix}5 \cdot 1 - 4 \cdot 2 \\4 \cdot 3 - 6 \cdot 1 \\6 \cdot 2 - 5 \cdot 3\end{pmatrix}=\begin{pmatrix}-3 \\6 \\-3\end{pmatrix}$

Das ist also ein senkrechter Vektor zu $\vec{a}$ und $\vec{b}$ . Das reicht als Antwort auf die Aufgabe.
Falls du aber sichergehen möchtest, dass du dich nicht verrechnet hast, kannst du ganz einfach mit dem Skalarprodukt überprüfen, ob der Vektor auch wirklich senkrecht auf $\vec{a}$ und $\vec{b}$ steht.
$\vec{a} \circ\begin{pmatrix}-3 \\6 \\-3\end{pmatrix}=\begin{pmatrix}6 \\5 \\4\end{pmatrix}\circ\begin{pmatrix}-3 \\6 \\-3\end{pmatrix}=6 \cdot (-3) + 5 \cdot 6 + 4 \cdot (-3) = -18 + 30 - 12 = 0$

$\vec{b} \circ\begin{pmatrix}-3 \\6 \\-3\end{pmatrix}=\begin{pmatrix}3 \\2 \\1\end{pmatrix}\circ\begin{pmatrix}-3 \\6 \\-3\end{pmatrix}=3 \cdot (-3) + 2 \cdot 6 + 1 \cdot (-3) = -9 + 12 - 3 = 0$

Das Skalarprodukt ist in beiden Fällen 0. Also ist der Vektor auf $\vec{a}$ und auf $\vec{b}$ senkrecht. Du hast dich also nicht verrechnet.
Hier ist jeder Vektor auf der -Achse eine richtige Antwort, weil diese senkrecht auf der – und der -Achse steht. Überprüfe aber am besten zur Übung, ob du mit dem Kreuzprodukt auf dasselbe Ergebnis kommst.
$\vec{a} \times \vec{b} =\begin{pmatrix}1 \\0 \\0\end{pmatrix}\times\begin{pmatrix}0 \\1 \\0\end{pmatrix}=\begin{pmatrix}0 \cdot 0 - 0 \cdot 1 \\0 \cdot 0 - 1 \cdot 0 \\1 \cdot 1 - 0 \cdot 0\end{pmatrix}=\begin{pmatrix}0 \\0 \\1\end{pmatrix}$

Das stimmt mit unserer vorherigen Überlegung überein.

Schnittgerade zweier Ebenen

im Videozum Video springen

Jetzt beherrschst du sämtliche Operationen der Vektorrechnung. Sehr gut gebrauchen kannst du dieses Wissen, wenn in deiner nächsten Prüfung nach der Schnittgeraden zweier Ebenen gefragt wird. Um darauf vorbereitet zu sein, solltest du dir unbedingt unser Video dazu ansehen.

Zum Video: Schnittgerade zweier Ebenen

zur Videoseite: Vektorrechnung

Beliebte Inhalte aus dem Bereich Lineare Algebra

Vektor berechnen

Vektoren addieren und subtrahieren

Lineare Unabhängigkeit und lineare Abhängigkeit von Vektoren

Linearkombination

Mittelpunkt einer Strecke berechnen

Thema präsentiert von unserem Werbepartner

Zur Webseite

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Bitte .