Differentialrechnung
In diesem Artikel gehen wir auf alle wichtigen Begriffe zur Differentialrechnung ein. Dabei klären wir die Zusammenhänge zwischen den einzelnen Themen und verschaffen dir so einen guten Gesamtüberblick zur Differentialrechnung.
Du hättest gern alle wichtigen Themen zur Differentialrechnung kurz und kompakt zusammengefasst? Dann schau dir einfach unser Video zur Differentialrechnung an. Dort erklären wir dir anschaulich alle Zusammenhänge.
Inhaltsübersicht
Differentialrechnung einfach erklärt
Die Differentialrechnung ist ein mathematisches Themengebiet aus dem Bereich der Analysis und beschäftigt sich mit den Änderungsraten von Funktionen. Im Mittelpunkt steht dabei die Ableitung .
Die Ableitung einer Funktion an einer Stelle entspricht geometrisch gesehen der dortigen Tangentensteigung. Diese kannst du anhand des Differentialquotienten bestimmen. Bei der Tangente handelt es sich dabei um den Graph der Linearisierung an dieser Stelle.
Differenzenquotient
Bevor wir auf den Begriff des Differentialquotienten weiter eingehen, betrachten wir zunächst einmal den Differenzenquotient .
Der Differenzenquotient

beschreibt die Steigung der Sekante durch den Punkt  und
und 
Diese bestimmst du mit Hilfe des Steigungsdreiecks unterhalb der Sekante. Das heißt du rechnest die Höhe des Dreiecks geteilt durch seine Länge und erhältst so die obige Formel.
Als nächstes sehen wir uns den bereits erwähnten zentralen Begriff der Differentialrechnung, den Differentialquotienten, an.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Differentialquotient
Für den Differentialquotient
betrachtest du den Grenzwert des Differenzenquotienten für 
Der Differentialquotient

beschreibt die Steigung der Tangente an der Stelle 
Was bei dieser Grenzwertbetrachtung passiert ist folgendes:
 bewegt sich auf
bewegt sich auf  zu. Dadurch nähert sich auch der Funktionswert
zu. Dadurch nähert sich auch der Funktionswert  dem Wert
dem Wert  . Insgesamt wird also der Punkt
. Insgesamt wird also der Punkt  entlang dem Funktionsgraphen von
entlang dem Funktionsgraphen von  in Richtung
in Richtung  geschoben. Die Punkte
geschoben. Die Punkte  und
und  bleiben dabei die ganze Zeit über eine Gerade verbunden. Wenn schließlich der Abstand zwischen
bleiben dabei die ganze Zeit über eine Gerade verbunden. Wenn schließlich der Abstand zwischen  und
und  gegen null geht, entspricht die Sekante durch
gegen null geht, entspricht die Sekante durch  und
und  der Tangente an der Stelle
der Tangente an der Stelle  und du hast somit über den Differenzenquotient ihre Steigung berechnet.
und du hast somit über den Differenzenquotient ihre Steigung berechnet.
Im Folgenden betrachten wir einen Begriff, der sehr häufig in der Differentialrechnung verwendet wird.
h Methode
Eine andere Interpretation des Differentialquotienten – jedoch mit dem gleichen Ergebnis – ist die h Methode .
Die h Methode

beschreibt die Steigung der Tangente an der Stelle 
Du kannst das im Abschnitt Differentialquotient beschriebene Vorgehen auch so auffassen, dass, wenn  auf
auf  zu läuft, sich der Abstand zwischen
zu läuft, sich der Abstand zwischen  und
und  immer mehr verringert. In diesem Fall betrachtest du nicht mehr den Grenzwert für
immer mehr verringert. In diesem Fall betrachtest du nicht mehr den Grenzwert für  , sondern du lässt den Abstand
, sondern du lässt den Abstand

gegen Null laufen, also  Dementsprechend ersetzt du nun in der Formel für den Differentialquotienten
Dementsprechend ersetzt du nun in der Formel für den Differentialquotienten  durch
durch  und
und  durch
durch  . Das Ergebnis ist die h Methode.
. Das Ergebnis ist die h Methode.
Auch der folgende Begriff der Differentialrechnung beruht auf dem Differentialquotienten.
Ableitungsfunktion und Ableitungsregeln
Wenn eine Funktion  an jeder Stelle
an jeder Stelle  ihres Definitionsbereichs differenzierbar ist, besitzt sie eine Ableitungsfunktion
ihres Definitionsbereichs differenzierbar ist, besitzt sie eine Ableitungsfunktion 
Die Ableitungsfunktion  ordnet jeder Stelle x den Wert des Differentialquotienten an dieser Stelle zu.
ordnet jeder Stelle x den Wert des Differentialquotienten an dieser Stelle zu.
Allerdings wäre es sehr aufwändig, wenn du jedes mal den Differentialquotient bestimmen müsstest, wenn du die Ableitung an einer Stelle wissen möchtest.
Stattdessen gibt es in der Differentialrechnung Ableitungsregeln
, die dir direkt die Ableitungsfunktion  liefern. Wenn du dann die Ableitung an einer bestimmten Stelle
liefern. Wenn du dann die Ableitung an einer bestimmten Stelle  wissen möchtest, musst du lediglich
wissen möchtest, musst du lediglich  in den Funktionsterm von
in den Funktionsterm von  einsetzen.
einsetzen.
Es gibt folgende wichtige Ableitungsregeln:
| Ableitungsregel | Funktion | Ableitung |
| Potenzregel |  |
 |
| Faktorregel | 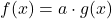 |
 |
| Summenregel |  |
 |
| Differenzregel |  |
 |
| Produktregel |  |
 |
| Quotientenregel |  |
![Rendered by QuickLaTeX.com f'(x)=\frac{g'(x)\cdot h(x)-g(x)\cdot h'(x)}{[h(x)]^2}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1128d60300515aa8b8df5c88d4dbbdf9_l3.png) |
| Kettenregel |  |
 |
Zudem gibt es noch bestimmte Funktionen, deren Ableitungen du unbedingt kennen solltest. Wir behandeln dabei jede Funktion in einem extra Artikel und zeigen dir viele Beispiele. Schau dir dazu die folgenden Artikel und Videos an:
Höhere Ableitungen
Wenn du eine Funktion öfter als nur einmal ableitest, spricht man von einer höheren Ableitung.
Angenommen du hast eine Funktion  und berechnest mit den eben erwähnten Ableitungsregeln die Ableitungsfunktion
und berechnest mit den eben erwähnten Ableitungsregeln die Ableitungsfunktion  Wenn
Wenn  differenzierbar ist, kannst du auch
differenzierbar ist, kannst du auch  nochmals ableiten. Das Ergebnis ist die zweite Ableitung
nochmals ableiten. Das Ergebnis ist die zweite Ableitung  . Solange die Ableitungsfunktion differenzierbar ist, kannst du sie beliebig oft ableiten. Sieh dir zum Beispiel die Funktion
. Solange die Ableitungsfunktion differenzierbar ist, kannst du sie beliebig oft ableiten. Sieh dir zum Beispiel die Funktion

an. Diese Funktion kannst du beliebig oft ableiten:




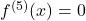

Wie du siehst, schreibt man bei höheren Ableitungen in den Exponent von  die Zahl der Ableitung in eine Klammer. In diesem Beispiel erhältst du ab der vierten Ableitung immer die Nullfunktion, wenn du erneut ableitest.
die Zahl der Ableitung in eine Klammer. In diesem Beispiel erhältst du ab der vierten Ableitung immer die Nullfunktion, wenn du erneut ableitest.
Solche unendlich oft differenzierbare Funktionen werden in der Differentialrechnung glatt genannt.
Extremwertaufgaben
Vielleicht fragst du dich wozu du die Differentialrechnung, insbesondere die Ableitung und höhere Ableitungen benötigst?
Eine Antwort darauf sind Extremwertaufgaben. Das heißt Aufgaben, in denen du Hochpunkte und Tiefpunkte oder eventuell Terrassenpunkte bestimmen sollst.
Häufig führst du für Aufgaben dieser Art eine sogenannte Kurvendiskussion durch. Mit den daraus gewonnenen Informationen kannst du den Verlauf des Funktionsgraphen skizzieren und erhältst so Informationen über die gesuchten Extremwerte.
Ableitungen finden natürlich nicht nur im Rahmen von Extremwertaufgaben ihre Anwendung, sondern spielen auch in den folgenden zwei zentralen Sätzen der Differentialrechnung eine zentrale Rolle.
Mittelwertsatz der Differentialrechnung
Der Mittelwertsatz zählt zu den wichtigsten Sätzen der Differentialrechnung.
Angenommen du betrachtest eine stetige Funktion  auf einem abgeschlossenen Intervall
auf einem abgeschlossenen Intervall ![Rendered by QuickLaTeX.com [a,b],](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3587445823432f044f4f460ccd1b6aa6_l3.png) welche auf
welche auf  differenzierbar ist.
differenzierbar ist.
Dann gibt es eine Stelle ![Rendered by QuickLaTeX.com x_0 \in [a,b],](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ee8840368c1aaea6f8dd50ae6405ddf8_l3.png) die eine Ableitung
die eine Ableitung

besitzt.
Das heißt es gibt eine Stelle  an der die Tangente die selbe Steigung besitzt, wie die Sekante durch die Punkte
an der die Tangente die selbe Steigung besitzt, wie die Sekante durch die Punkte  und
und 
Hauptsatz der Differential- und Integralrechnung (HDI)
Die Differentialrechnung ist eng verwandt mit der Integralrechnung , wie auch der folgende Hauptsatz der Differentialrechnung verdeutlicht.
Angenommen du hast eine auf einem Intervall  stetige Funktion
stetige Funktion  und einen beliebigen Punkt
und einen beliebigen Punkt ![Rendered by QuickLaTeX.com a \in [a,b]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c41a0967a101a2c2697e980c8c574511_l3.png) gegeben.
gegeben.
Dann ist die Funktion

auf  differenzierbar und für ihre Ableitung gilt
differenzierbar und für ihre Ableitung gilt 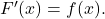
Man nennt in der Differentialrechnung  eine Stammfunktion
von
eine Stammfunktion
von 
Damit ergibt sich die bekannte Formel zum Berechnen bestimmter Integrale , nämlich:

Im Folgenden werden wir uns ansehen, wie in der Differentialrechnung mit mehrdimensionalen Funktionen umgegangen wird.
Partielle Ableitungen
Bisher haben wir nur eindimensionale reellwertige Funktionen betrachtet, also solche die von einem Intervall  in die reellen Zahlen
in die reellen Zahlen  abbilden. Das heißt die Funktion hing nur von einer Variable
abbilden. Das heißt die Funktion hing nur von einer Variable  ab.
ab.
Jetzt sehen wir uns Funktionen an, die von einer Teilmenge des  nach
nach  abbilden. Das heißt Funktionen, die von mehreren Variablen
abbilden. Das heißt Funktionen, die von mehreren Variablen 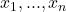 abhängen. Sei also
abhängen. Sei also

eine solche Funktion. Wie leitest du  nun ab?
nun ab?
Du kannst die partiellen Ableitungen
von  bilden. In so einem Fall nimmst du eine Variable
bilden. In so einem Fall nimmst du eine Variable  , und leitest dann deine Funktion nach dieser Variablen ab. Alle anderen n-1 Variablen behandelst du wie Konstanten.
, und leitest dann deine Funktion nach dieser Variablen ab. Alle anderen n-1 Variablen behandelst du wie Konstanten.
Das Ergebnis ist die i-te partielle Ableitung von 

Sie gibt dir die lokale Änderungsrate entlang der i-ten Koordinatenachse an. Für eine geometrische Anschauung sieh dir den extra Artikel zu den partiellen Ableitungen an.
Damit klarer wird, wie du diese Ableitungen bestimmst, rechnen wir ein Beispiel. Gegeben ist die Funktion

Du bestimmst nun all ihre partiellen Ableitungen



Diese berechnest du mit den üblichen Ableitungsregeln der Differentialrechnung.
Nun kannst du deine Ergebnisse noch als Spaltenvektor, den sogenannten Gradienten von f, festhalten:
![Rendered by QuickLaTeX.com \nabla f(x) = \left(\begin{array}{c} \frac{\partial f}{\partial x_1} \\[0.5em] \frac{\partial f}{\partial x_2}\\[0.5em] \frac{\partial f}{\partial x_3}\end{array}\right)= \left(\begin{array}{c} 2-5x_3 \\[0.5em] 12x_2^2\\[0.5em] -5x_1\end{array}\right).](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3f2fc06f972e1e1498a38f569dcc973b_l3.png)
Dieser Vektor zeigt in die Richtung des größten Anstiegs der Funktion  an der Stelle
an der Stelle 
Die partiellen Ableitungen sind ein Spezialfall des nun folgenden Ableitungsbegriffs der Differentialrechnung.
Richtungsableitungen
Wir bleiben bei Funktionen, die von mehreren Variablen abhängen und betrachten deren Richtungsableitungen .
Also angenommen du hast erneut eine reellwertige Funktion

und dazu noch eine Richtung, nämlich den Vektor 
 mit Länge eins, gegeben.
mit Länge eins, gegeben.
Dann lautet die Richtungsableitung von  an der Stelle
an der Stelle  :
:

Diese Richtungsableitung  gibt die lokale Änderungsrate bei einer Bewegung in Richtung
gibt die lokale Änderungsrate bei einer Bewegung in Richtung  im Punkt
im Punkt  an.
an.
Wählst du also als  einen Einheitsvektor
einen Einheitsvektor  , dann erhältst du die lokale Änderungsrate entlang einer Koordinatenrichtung, also die partielle Ableitung.
, dann erhältst du die lokale Änderungsrate entlang einer Koordinatenrichtung, also die partielle Ableitung.
Schließlich sehen wir uns noch einen letzten Begriff der Differentialrechnung an, nämlich die totale Differenzierbarkeit .
Differentialrechnung — häufigste Fragen
(ausklappen)
Differentialrechnung — häufigste Fragen
(ausklappen)-
Was bedeutet die Ableitung geometrisch am Graphen?Die Ableitung an einer Stelle bedeutet geometrisch die Steigung der Tangente am Graphen genau dort. Sie beschreibt also, wie stark der Graph an dieser Stelle ansteigt oder fällt. Die Tangente ist dabei der Graph der Linearisierung an dieser Stelle.
-
Wie unterscheide ich Sekante und Tangente bei einer Funktion?Eine Sekante verbindet zwei verschiedene Punkte des Funktionsgraphen, eine Tangente berührt den Graphen in einem Punkt. Deshalb beschreibt die Sekante eine mittlere Steigung zwischen
 und
und  , während die Tangente die Steigung genau an
, während die Tangente die Steigung genau an  angibt, wenn
angibt, wenn  .
.
-
Warum wird aus dem Differenzenquotienten im Grenzwert der Differentialquotient?Aus dem Differenzenquotienten wird im Grenzwert der Differentialquotient, weil die Sekante beim Grenzübergang zur Tangente wird. Wenn
 auf
auf  zuläuft, rückt der Punkt
zuläuft, rückt der Punkt  an
an  heran. Für
heran. Für  liefert die Sekantensteigung die Tangentensteigung.
liefert die Sekantensteigung die Tangentensteigung.
-
Wie hängt die h Methode mit dem Differentialquotienten zusammen?Die h Methode ist dieselbe Grenzwert-Idee wie der Differentialquotient, nur mit dem Abstand
 . Statt
. Statt  betrachtet man
betrachtet man  und schreibt
und schreibt  als
als  . So entsteht
. So entsteht  .
.
-
Wann ist eine Funktion an einer Stelle differenzierbar?Eine Funktion ist an der Stelle
 differenzierbar, wenn der Grenzwert
differenzierbar, wenn der Grenzwert  existiert. Dann lässt sich der Differentialquotient an
existiert. Dann lässt sich der Differentialquotient an  berechnen. Das Ergebnis ist
berechnen. Das Ergebnis ist  , also die Ableitung an dieser Stelle.
, also die Ableitung an dieser Stelle.
Totale Differenzierbarkeit
Bis hierhin haben wir nur Funktionen betrachtet, die in den eindimensionalen reellen Raum, also  , abbilden. Jetzt sehen wir uns auch Funktionen an, die nicht nur von mehreren Variablen abhängen, sondern auch noch in den mehrdimensionalen reellen Raum
, abbilden. Jetzt sehen wir uns auch Funktionen an, die nicht nur von mehreren Variablen abhängen, sondern auch noch in den mehrdimensionalen reellen Raum  abbilden.
abbilden.
Wir betrachten also eine Funktion der Form:

 ist an der Stelle
ist an der Stelle  total differenzierbar, wenn es eine lineare Abbildung
total differenzierbar, wenn es eine lineare Abbildung  gibt, sodass
gibt, sodass

gilt.
Die lineare Abbildung  kann als
kann als  Matrix dargestellt werden. Die Ableitung von f wird in der Differentialrechnung Jacobi-Matrix
genannt und entspricht in diesem Fall der totalen Ableitung.
Matrix dargestellt werden. Die Ableitung von f wird in der Differentialrechnung Jacobi-Matrix
genannt und entspricht in diesem Fall der totalen Ableitung.
Angenommen du hast eine total differenzierbare Funktion  gegeben. Dann kannst du ihr sogenanntes totales Differential
:
gegeben. Dann kannst du ihr sogenanntes totales Differential
:

berechnen. Dieser Begriff der Differentialrechnung verrät dir, wie sich die Funktion bei kleinen Abweichungen in den Variablen verändert.


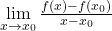
 , also die Ableitung von
, also die Ableitung von 
