Bruch ableiten
Wenn du dir nicht mehr sicher bist, wie du einen Bruch ableiten kannst, bist du hier genau richtig. Schaue dir auch unser passendes Video an.
Inhaltsübersicht
Bruch ableiten einfach erklärt
Es gibt für verschiedene Arten von Funktionen verschiedene Ableitungsregeln. Wenn du einen Bruch ableiten musst und sowohl über als auch unter dem Bruchstrich ein x steht, dann brauchst du die Quotientenregel.
Du benutzt die Ableitungsregel also, wenn du eine Funktion f(x) hast, die im Zähler g(x) und im Nenner h(x) ein x enthält. Um dir Schreibarbeit zu sparen, kannst du hier auch die Klammern weglassen.
![Rendered by QuickLaTeX.com \[ f(x) = \frac{g(x)}{h(x)} \quad\hat{=}\quad f = \frac{g}{h} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2200cb995dbabcab8e6caa85f56c3c94_l3.png)
Wenn du eine Funktion f ableiten möchtest, die im Nenner h und im Zähler g von x abhängen, brauchst du die Formel:
![Rendered by QuickLaTeX.com \[ f = \frac{\textcolor{red}{g}}{\textcolor{blue}{h}} \quad\Longrightarrow\quad f' = \frac{\textcolor{blue}{h}\cdot \textcolor{orange}{g'} - \textcolor{teal}{h'} \cdot \textcolor{red}{g}}{\textcolor{blue}{h}^2} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0a5212a36da347405dd82f561a480bc8_l3.png)
Bruch ableiten Beispiel
Mathe verstehst du am besten mit einem Beispiel: Schaue dir die Funktion
![Rendered by QuickLaTeX.com \[ f(x) = \frac{x^5 + 1}{x^2} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-32869f8f97543ae7854e31add0c179ba_l3.png)
an. Wenn du diesen Bruch ableiten willst, brauchst du die Quotientenregel, weil sowohl im Zähler  als auch im Nenner
als auch im Nenner  ein x steht.
ein x steht.
1. Schritt: Teilfunktionen g und h ableiten
Leite zuerst den Nenner und Zähler getrennt voneinander ab. Dafür schreibst du sie dir als eigene Funktionen auf und nennst den Zähler g. Der Nenner heißt ab jetzt h.
![Rendered by QuickLaTeX.com \[ \textcolor{red}{g = x^5 +1} \qquad \textcolor{blue}{h = x^2} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-56401fd28318d21cf040e2037b45c0d6_l3.png)
Leite beide Seiten mit der Potenzregel ab. Falls du die nicht mehr ganz im Kopf hast, kannst du hier spicken.
![Rendered by QuickLaTeX.com \[ \textcolor{orange}{g' = 5x^4} \qquad \textcolor{teal}{h' = 2x} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c0e0a148119ac4f7ce682abc60a84cbd_l3.png)
2. Schritt: Zwischenergebnis in die Formel einsetzen
Als nächstes musst du die Teilfunktionen und ihre Ableitungen in die Formel einsetzen, um den Bruch ableiten zu können. Ganz wichtig: Klammern nicht vergessen!

3. Schritt: Terme vereinfachen
Anschließend kannst du den Bruch noch etwas vereinfachen. Falls du dabei noch etwas Übung brauchst, haben wir für dich ein Video über das Vereinfachen von Termen vorbereitet. Hier musst du zuerst die Klammer ausmultiplizieren und die Potenzen im Nenner multiplizieren.
![Rendered by QuickLaTeX.com \[ f' = \frac{x^2\cdot 5x^4 - \textcolor{olive}{2x \cdot (x^5 +1)}}{\textcolor{olive}{(x^2)^2}} = \frac{ x^2\cdot5x^4 - \textcolor{olive}{2x^6 - 2x} }{\textcolor{olive}{x^4}} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d8ea6b6cc903f624d1b920ae927f6ec3_l3.png)
Als nächstes kannst du multiplizieren und subtrahieren. Zuletzt kannst du den Bruch mit x kürzen.
![Rendered by QuickLaTeX.com \[ f' = \frac{ \textcolor{olive}{x^2\cdot5x^4 - 2x^6} - 2x }{x^4} = \frac{ \textcolor{olive}{5x^6 - 2x^6} - 2x }{x^4} = \frac{ \textcolor{olive}{3x^6} - 2x }{x^4} = \frac{ 3x^5 - 2 }{x^3} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c51460d3a33b2b7e85eb575040d1e394_l3.png)
Die Ableitung von f ist also:
![Rendered by QuickLaTeX.com \[ f(x) = \frac{x^5 + 1}{x^2} \quad\Longrightarrow\quad f'(x) = \frac{ 3x^5 - 2 }{x^3} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-361b2a9bc5d3ff69a5f697f8d4e57a79_l3.png)
Brüche ableiten ist gar nicht so schwer, oder? Wie wäre es mit einem zweiten Beispiel?
![Rendered by QuickLaTeX.com \[ f(x) = \frac{e^x}{x} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2dd346b1d0a34e954cb70399046fdc20_l3.png)
1. Schritt: Leite Nenner und Zähler ab.

2. Schritt: Setze in die Quotientenregel ein.

3. Schritt: Vereinfache die Terme, indem du  ausklammerst.
ausklammerst.
![Rendered by QuickLaTeX.com \[ f'(x) = \frac{(x-1)\cdot e^x }{x^2} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-866702cfb2d6e8bed1661dfb4221b636_l3.png)
Die Ableitung von f ist also:
![Rendered by QuickLaTeX.com \[ f(x) = \frac{e^x}{x} \quad\Longrightarrwo\quad f'(x) &= \frac{(x-1)\cdot e^x }{x^2} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8df05215e81eb4c1476ebfd9351565b1_l3.png)
Das wird doch mit jedem Beispiel einfacher, oder? Jetzt bist du für alle Aufgaben gewappnet!
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Quotientenregel Herleitung
Die Quotientenregel ist nur eine Abkürzung für die Produkt- und Kehrwertregel. Aber wie kommst du von den anderen Ableitungsregeln zur Regel fürs Bruch ableiten? Angenommen, du willst einen Bruch ableiten:
![Rendered by QuickLaTeX.com \[ f = \frac{\textcolor{red}{g}}{\textcolor{blue}{h}} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-e61af5d4335d909b7e2be342571df0ee_l3.png)
Dann kannst du ihn auch als Produkt schreiben und mit der Produktregel ableiten.
![Rendered by QuickLaTeX.com \[ f' = (\textcolor{red}{g} \cdot \textcolor{blue}{h^{-1}})' = \textcolor{red}{g} \cdot \textcolor{teal}{(h^{-1})'} + \textcolor{orange}{g'}\cdot \textcolor{blue}{h^{-1}} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-98585d26addfc173899c7a430b711157_l3.png)
Die Kehrwertregel sagt dir, dass  ist.
ist.
![Rendered by QuickLaTeX.com \[ f' = \textcolor{red}{g} \cdot \frac{-\textcolor{teal}{h'}}{\textcolor{blue}{h}^2} + \textcolor{orange}{g'}\cdot \textcolor{blue}{h^{-1}} = \frac{-\textcolor{red}{g}\cdot \textcolor{teal}{h'}}{\textcolor{blue}{h}^2} + \frac{\textcolor{orange}{g'}}{\textcolor{blue}{h}} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-eb4492b97f256b8896d9fde48ef2a8f1_l3.png)
Wenn du den rechten Bruch mit h erweiterst, kannst du die ganze Formel in einen Bruch schreiben und hast damit den Beweis für die Quotientenregel-Formel.
![Rendered by QuickLaTeX.com \[ f' = \frac{-\textcolor{red}{g}\cdot \textcolor{teal}{h'}}{\textcolor{blue}{h}^2} + \frac{\textcolor{orange}{g'} \cdot \textcolor{blue}{h}}{\textcolor{blue}{h}\cdot \textcolor{blue}{h}} = \frac{ \textcolor{orange}{g'}\textcolor{blue}{h} - \textcolor{red}{g}\textcolor{teal}{h'} }{\textcolor{blue}{h}^2} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5043098e02b03ccc5db9b10d4ffcf024_l3.png)
Bruch ableiten — häufigste Fragen
(ausklappen)
Bruch ableiten — häufigste Fragen
(ausklappen)-
Wann brauche ich die Quotientenregel wirklich nicht, obwohl ein Bruch da steht?Du brauchst die Quotientenregel nicht, wenn nur Zähler oder nur Nenner von x abhängt. Dann kannst du den Bruch als Faktor schreiben und mit Potenz-, Produkt- oder Kettenregel ableiten. Beispiel:
 .
.
-
Wie merke ich mir, welcher Term beim Zähler-Nenner-Teil in der Quotientenregel das Minus bekommt?Das Minus steht beim Produkt aus Nenner-Ableitung und ursprünglichem Zähler:
 . Merkhilfe: „Erst Nenner mal Zähler-Ableitung, minus Nenner-Ableitung mal Zähler“. So bleibt die Reihenfolge immer gleich.
. Merkhilfe: „Erst Nenner mal Zähler-Ableitung, minus Nenner-Ableitung mal Zähler“. So bleibt die Reihenfolge immer gleich.
-
Welche Fehler passieren am häufigsten bei Klammern und Vorzeichen in der Quotientenregel?Am häufigsten werden Klammern um
 oder
oder  vergessen, sodass beim Ausmultiplizieren Vorzeichen falsch werden. Außerdem wird das Minus oft nicht auf alle Summanden im Zähler verteilt. Beispiel:
vergessen, sodass beim Ausmultiplizieren Vorzeichen falsch werden. Außerdem wird das Minus oft nicht auf alle Summanden im Zähler verteilt. Beispiel:  wird fälschlich zu
wird fälschlich zu  statt korrekt zu
statt korrekt zu  .
.
-
Wie leite ich einen Bruch ab, wenn im Zähler oder Nenner noch eine Kettenregel steckt?Du wendest die Quotientenregel an und leitest
 und/oder
und/oder  jeweils mit der Kettenregel ab. Entscheidend ist:
jeweils mit der Kettenregel ab. Entscheidend ist:  und
und  sind vollständige Ableitungen, inklusive „innerer Ableitung“. Beispiel: Bei
sind vollständige Ableitungen, inklusive „innerer Ableitung“. Beispiel: Bei  ist
ist  .
.
-
Was mache ich, wenn ich nach dem Ableiten noch kürzen will und nicht sicher bin, ob das erlaubt ist?Kürzen ist erlaubt, wenn Zähler und Nenner einen gemeinsamen Faktor haben, der komplett ausgeklammert ist. Kürze nie Summen über ein Plus/Minus hinweg, also nicht „termweise“. Beispiel:
 ist ok, aber
ist ok, aber  darfst du nicht zu
darfst du nicht zu  „kürzen“.
„kürzen“.
Weitere Ableitungsregeln
Die Quotientenregel ist eine von vielen Ableitungsregeln der Differentialrechnung. Damit du alle Funktionen ableiten kannst, musst du auch alle anderen Regeln kennen. Schaue dir gleich noch unsere Videos zu den anderen Ableitungsregeln an!
| Ableitungsregel | Funktion | Ableitung |
| Produktregel |  |
 |
| Summenregel |  |
 |
| Differenzregel |  |
 |
| Kettenregel |  |
 |
| Potenzregel |  |
 |
| Faktorregel | 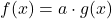 |
 |