Video

Quiz

Hier geht's zum Video „Wendepunkt berechnen“

Sattelpunkt berechnen

Wichtige Inhalte in diesem Video

Sattelpunkt einfach erklärt

Sattelpunkt berechnen: Schritt-für-Schritt Anleitung

Du möchtest wissen, was Sattelpunkte sind und wie du sie bestimmst? Im folgenden Artikel erklären wir dir Schritt für Schritt wie du einen Sattelpunkt berechnen kannst.

Möchtest du zum Thema Sattelpunkt berechnen lieber ein Video sehen? Kein Problem! Schau dir unser Video an, um das Thema in kurzer Zeit zu verstehen.

Inhaltsübersicht

Sattelpunkt einfach erklärt

im Videozur Stelle im Video springen

Stell dir vor du fährst mit dem Fahrrad einen Hügel hinunter und zwischendurch gibt es einen Punkt, an dem du ohne Probleme stehen bleiben kannst, bevor du dann weiter hinunterfährst. Das ist der Punkt der als Sattelpunkt oder als Terrassenpunkt bezeichnet wird.

Sattelpunkt, Terrassenpunkt, Wendepunkt, Wendestelle, Sattelpunkt berechnen, Terrassenpunkt berechnen — Der Sattelpunkt einer Funktion

Das heißt, beim Sattelpunkt hat die Funktion eine Steigung von 0, während der Graph sowohl davor als auch danach fällt (oder steigt).

Ein Sattelpunkt ist ein Wendepunkt mit waagerechter Tangente. Das bedeutet, dass zu den Bedingungen eines Wendepunktes f''(x_0)=0 und $f'''(x_0) \neq 0$ noch zusätzlich die erste Ableitung f'(x_0) null sein muss:

Sattelpunkt Bedingungen

und $f'''(x_0) \neq 0$

Sattelpunkt berechnen: Schritt-für-Schritt Anleitung

im Videozur Stelle im Video springen

Nun erklären wir dir Schritt für Schritt, wie du die Sattelpunkte einer Funktion f(x) berechnen kannst.

Schritt 1: Berechne die ersten drei Ableitungen der Funktion f(x).

Schritt 2: Ermittle die Nullstellen x_0 der zweiten Ableitung $f^{\prime \prime}(x)$ .

Schritt 3: Setze die Nullstellen der zweiten Ableitung in die dritte Ableitung $f^{\prime \prime \prime}(x)$ ein. Ist $f^{\prime \prime \prime}(x_0) \neq 0$ , so handelt es sich um Wendestellen.

Schritt 4: Setze die Wendestellen in die erste Ableitung $f^{\prime}(x)$ ein. Ist $f^{\prime}(x_0) = 0$ , so hat f an der Stelle x_0 einen Sattelpunkt. (Dieser Schritt ist der einzige Unterschied zum Wendepunkt berechnen )

Schritt 5: Nun setzt du die x-Werte aus Schritt 4 in die Funktion f(x) ein, um die y-Koordinaten zu bestimmen.

Beispiel

Um die Herangehensweise besser zu verstehen, schauen wir uns ein konkretes Beispiel dazu an.

Betrachte dazu die Funktion

$f(x) = -\frac{1}{4}x^4+ \frac{3}{2}x^2+2x+ \frac{3}{4}.$

Schritt 1: Zuerst berechnest du die Ableitungen der Funktion f

$f^{\prime}(x) = -x^3+3x+2$

$f^{\prime \prime}(x) = -3x^2+3$

$f^{\prime \prime \prime}(x) = -6x.$

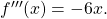
Schritt 2: Nun benötigst du die Nullstellen der zweiten Ableitung. Dafür setzt du $f^{\prime \prime}(x) = -3x^2+3 = 0$ und bekommst dafür

x_1 = -1

x_2 = 1.

Schritt 3: Setze die ermittelten Werte in die dritte Ableitung ein. Dabei erhältst du

$f^{\prime \prime \prime}(x_1) = -6 \cdot (-1) = 6$

$f^{\prime \prime \prime}(x_2) = -6 \cdot 1 = -6$

Da beide Werte ungleich 0 sind, befinden sich an den Stellen Wendepunkte.

Schritt 4: Jetzt überprüfst du noch, ob es sich dabei um Terrassenpunkte handelt. Dafür setzt du die ermittelten Werte x_1 und x_2 in $f^{\prime}$ ein

$f^{\prime}(x_1) = -(-1)^3+3 \cdot (-1) +2 = 0$

$f^{\prime}(x_2) = -1^3+3 \cdot 1+2 = 4 \neq 0.$

Das bedeutet also, dass du für x_1 = -1 einen Sattelpunkt hast, aber nicht für x_2 = 1 .

Schritt 5: Nun kannst du noch die y-Koordinate vom Sattelpunkt berechnen. Dafür wertest du einfach f an der Stelle x_1 = -1 aus

$f(x_1) = -\frac{1}{4} \cdot (-1)^4 + \frac{3}{2} \cdot (-1)^2 + 2 \cdot (-1) + \frac{3}{4} = 0.$

Somit hast du den Sattelpunkt $S(-1 \vert 0)$ berechnet.

Sattelpunkt, Terrassenpunkt, Wendepunkt, Wendestelle, Sattelpunkt berechnen, Terrassenpunkt berechnen — Der Sattelpunkt der Funktion f

Was ist ein Sattelpunkt?

Jetzt weißt du, wie du einen Sattelpunkt berechnen kannst, aber was genau passiert da?

Angenommen die Funktion f fällt vor dem Terrassenpunkt. Da der Sattelpunkt eine Steigung von 0 hat, muss die Steigung vor dem Terrassenpunkt zunehmen, das heißt die Funktion ist in dem Bereich linksgekrümmt. Nach dem Sattelpunkt fällt die Funktion und hat somit eine Rechtskrümmung. Das bedeutet, dass wir an der Stelle des Sattelpunktes eine Änderung des Krümmungsverhaltens haben und somit einen Wendepunkt. Daher überprüfst du für die Berechnung der Sattelpunkte die Bedingungen für einen Wendepunkt. Zusätzlich musst du dann bei den Wendepunkten noch überprüfen, ob hier die Steigung null ist. Trifft dies zu, dann handelt es sich um einen Sattelpunkt:

Merke

Um einen Sattelpunkt zu bestimmen, musst du die Sattelpunkt Bedingungen

$f^{\prime}(x_0) = 0$
$f^{\prime \prime }(x_0) = 0$ , $f^{\prime \prime \prime}(x_0) \neq 0$

überprüfen.

Hinweis: Die oberen Bedingungen sind hinreichend, aber nicht notwendig. Ist die dritte Ableitung 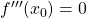$f^{\prime \prime \prime}(x_0) = 0$ , so gibt es trotzdem bestimmte Funktionen, die bei x_0 einen Sattelpunkt haben können. Um das zu überprüfen, setzt du x-Werte links und rechts von der kritischen Stelle in die zweite Ableitung $f^{\prime \prime}$ ein. Ist ein Wert positiv und einer negativ, so handelt es sich um einen Sattelpunkt.

Wenn du zum Beispiel die Funktion f(x) = x^5 betrachtest, so fällt dir auf, dass an der Stelle x=0 gilt

$f^{\prime}(0) = f^{\prime \prime}(0) = f^{\prime \prime \prime}(0) = 0.$

Also setzt du Werte links und rechts von x=0 in die zweite Ableitung $f^{\prime \prime}(x) = 20x^3$ ein und erhältst

$f^{\prime \prime}(-1) = -20 < 0$

$f^{\prime \prime}(1) = 20 > 0.$

Das heißt, wir haben an der Stelle x=0 einen Sattelpunkt.

Unterschied Sattelpunkt Wendepunkt

Der einzige Unterschied zwischen Sattel- und Wendepunkten ist die Steigung. Während am Wendepunkt eine beliebige Steigung vorliegen kann, ist es für Terrassenpunkte wichtig, dass die Steigung dort gleich 0 ist. Deshalb prüfst du, ob die erste Ableitung am Wendepunkt null ergibt.

Wichtige Begriffe der Kurvendiskussion

Bevor wir uns den Aufgaben widmen, geben wir dir an dieser Stelle eine kleine Übersicht wichtiger Begriffe, die du im Zusammenhang mit der Kurvendiskussion beherrschen solltest:

Kurvendiskussion
Kurvendiskussion Aufgaben
Ableitung
Ableitungsregeln
Extrempunkte berechnen
Hoch- und Tiefpunkte
Monotonie
Wendepunkt berechnen
Wendetangente
y Achsenabschnitt berechnen
Symmetrie
Punktsymmetrie
Achsensymmetrie

Sattelpunkt berechnen Aufgaben

Im Folgenden geben wir dir zwei Beispielaufgaben, womit du das Sattelpunkt Berechnen üben kannst.

Aufgabe 1: Sattelpunkt berechnen einer e Funktion

Betrachte die Funktion

f(x) = (2x^2-8x+10)e^x

Berechne die Koordinaten der Sattelpunkte, falls welche existieren.

Lösung Aufgabe 1

Als erstes berechnest du mithilfe der Produktregel die ersten drei Ableitungen. Damit erhältst du

$f^{\prime}(x) = (2x^2-4x+2)e^x$

$f^{\prime \prime}(x) = (2x^2-2)e^x$

$f^{\prime \prime \prime}(x) = (2x^2+4x -2)e^x$

Nun bestimmst du die Nullstellen der zweiten Ableitung, das heißt, du setzt

(2x^2-2)e^x = 0,

womit du die Nullstellen

x_1 = 1

x_2 = -1

bekommst. Setzt du jetzt x_1 und x_2 in $f^{\prime \prime \prime}(x)$ ein, so erhältst du

$f^{\prime \prime \prime}(x_1) = (2 \cdot 1^2+4 \cdot 1 -2) \cdot e^1 = 10,87 \neq 0$

$f^{\prime \prime \prime}(x_2) = (2 \cdot (-1)^2 + 4 \cdot (-1) - 2) \cdot e^{-1} = -1,47 \neq 0 .$

Damit hat die Funktion an beiden Stellen Wendepunkte. Du willst aber wissen, ob die Funktion Terrassenpunkte besitzt. Also setzt du noch zusätzlich die Werte x_1 und x_2 in die erste Ableitung ein

$f^{\prime}(x_1) = (2 \cdot 1^2-4 \cdot 1+2) \cdot e^1 = 0$

$f^{\prime}(x_2) = (2 \cdot (-1)^2-4 \cdot (-1)+2) \cdot e^{-1} = 2,94.$

Damit hast du einen Sattelpunkt für x_1=1 , aber nicht für x_2= -1 . Jetzt kannst du die Koordinaten vom Sattelpunkt berechnen, indem du x_1 in die Funktion f einsetzt

$f(x_1) = (2 \cdot 1^2 -8 \cdot 1 +10) \cdot e^1 = 10,87.$

Damit erhältst du $S(1 \vert 10,87)$ .

Aufgabe 2: Sattelpunkt einer gebrochenrationalen Funktion

Du hast folgende gebrochenrationale Funktion gegeben

$f(x) = \frac{(x-2)^3}{x^2}.$

Bestimme die Sattelpunkte der Funktion.

Lösung Aufgabe 2

Mithilfe der Quotienten – und Kettenregel berechnest du die Ableitungen der Funktion f

$f^{\prime}(x) = \frac{x^3-12x+16}{x^3}$

$f^{\prime \prime}(x) = \frac{24x-48}{x^4}$

$f^{\prime \prime \prime}(x) = \frac{-72x + 192}{x^5}.$

Jetzt musst du erstmal überprüfen, ob die Funktion Wendepunkte besitzt. Dazu setzt du die zweite Ableitung gleich null

$f^{\prime \prime}(x) = \frac{24x-48}{x^4} = 0$

und ermittelst somit die Nullstelle

x_0 = 2.

Um zu überprüfen, ob f bei x_0 einen Wendepunkt hat, setzt du den Wert x_0=2 in $f^{\prime \prime \prime}$ ein und erhältst

$f^{\prime \prime \prime}(x_0) = \frac{-72 \cdot 2 + 192}{2^5} = 1,5 \neq 0.$

Da es sich somit um eine Wendestelle handelt, kannst du nun die erste Ableitung überprüfen. Setzt du den Wert x_0 = 2 in $f^{\prime}$ ein, bekommst du

$f^{\prime}(x_1) = \frac{2^3 - 12 \cdot 2 +16}{2^3} = 0.$

Damit handelt es sich um einen Sattelpunkt. Indem du nun x_0 in die Funktion f einsetzt, kannst du den Sattelpunkt berechnen

$f(x_0) = \frac{(2-2)^3}{2^2} = 0.$

Damit ist bei $S(2 \vert 0)$ ein Terrassenpunkt.

Wendetangente

Super! Die Berechnung und Unterscheidung von Wende- und Sattelpunkten bereitet dir jetzt keine Probleme mehr. Du fragst dich was du damit jetzt machen sollst? Du kannst zum Beispiel die Wendetangente berechnen. Die Wendetangente ist eine lineare Funktion, die die Funktion f am Wendepunkt berührt. Dafür setzt du einfach den Wende- bzw. Sattelpunkt in die allgemeine Formel ein.

$y_{w}(x) = f^{\prime}(x_{w}) \cdot (x-x_{w}) + y_{w},$

Damit du keine Probleme mehr mit Aufgaben zur Kurvendiskussion hast, musst du dir auf jeden Fall unser Video zum Wendetangente berechnen anschauen!

Wendetangente, Wendetangente berechnen, Berechnung Wendetangente, Wendenormale — Zum Video: Wendetangente berechnen

zur Videoseite: Sattelpunkt berechnen

Beliebte Inhalte aus dem Bereich Analysis

Krümmungsverhalten

Wendepunkt berechnen

Wendetangente berechnen

Sattelpunkt berechnen

Thema präsentiert von unserem Werbepartner

Zur Webseite

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Bitte .