Extremstellen
Willst du wissen, was Extremstellen sind und wie du sie unterscheidest? Das lernst du in diesem Artikel und in unserem Video .
Inhaltsübersicht
Extremstellen einfach erklärt
Du betrachtest Extremstellen ganz oft, wenn du eine Kurvendiskussion in Mathe machst. Aber was sind Extremstellen überhaupt?
Stell dir vor, du wirfst einen Ball hoch in die Luft. Du kannst sehen, dass er irgendwann gar nicht mehr höher steigt, sondern runterfällt! Die Stelle, an der der Ball zwischen Steigen und Fallen wechselt, nennst du Extremstelle. So würde das in einem Funktionsgraphen aussehen:
Wenn du eine Tangente
an den Graphen legst, entspricht das genau der Steigung. Bei der Extremstelle H steigt der Ball weder, noch fällt er. Deshalb hat die Tangente eine Steigung von 0! Da du die momentane Steigung mit der ersten Ableitung berechnest, ergibt sich der Zusammenhang.
Merk dir: Bei einer Extremstelle xs ist die Ableitung immer gleich Null: f'(xs )=0
Du siehst an dem Beispiel, dass beim höchsten Punkt deine Extremstelle ist. Aber es gibt auch noch andere Typen von Extremstellen.
Extremstellen sind besondere Punkte im Verlauf einer Funktion, an denen sie ein lokales oder globales Maximum oder Minimum erreicht. An diesen Stellen ändert sich das Steigungsverhalten der Funktion, was sich häufig daran erkennen lässt, dass die erste Ableitung dort den Wert null hat und sich das Vorzeichen der zweiten Ableitung verändert.
Hochpunkt
Bei einem Hochpunkt steigt der Graph zuerst und fällt dann wieder. Wichtig ist, dass du hier zwei Sachen überprüfst:
- f'(xs) = 0
- f“(xs) < 0
Wie der Name schon sagt, ist das hier also vermutlich der höchste Punkt deines Graphen. Das stimmt aber nicht ganz! Es kann auch mehrere Hochpunkte geben. Erfüllt deine Extremstelle beide Bedingungen, hast du nur einen lokalen Hochpunkt. Das ist dann der höchste Punkt in der näheren Umgebung. Das bedeutet, dass alle Punkte, die nah an dem lokalen Hochpunkt liegen, alle tiefer liegen. Ist dieser Punkt tatsächlich der allerhöchste Punkt deines Graphen, bezeichnest du ihn als absoluten Hochpunkt.
Tiefpunkt
Bei einem Tiefpunkt ist genau das Gegenteil der Fall! Hier fällt der Graph zuerst und steigt dann wieder. Du prüfst dann:
- f'(xs) = 0
- f“(xs) > 0
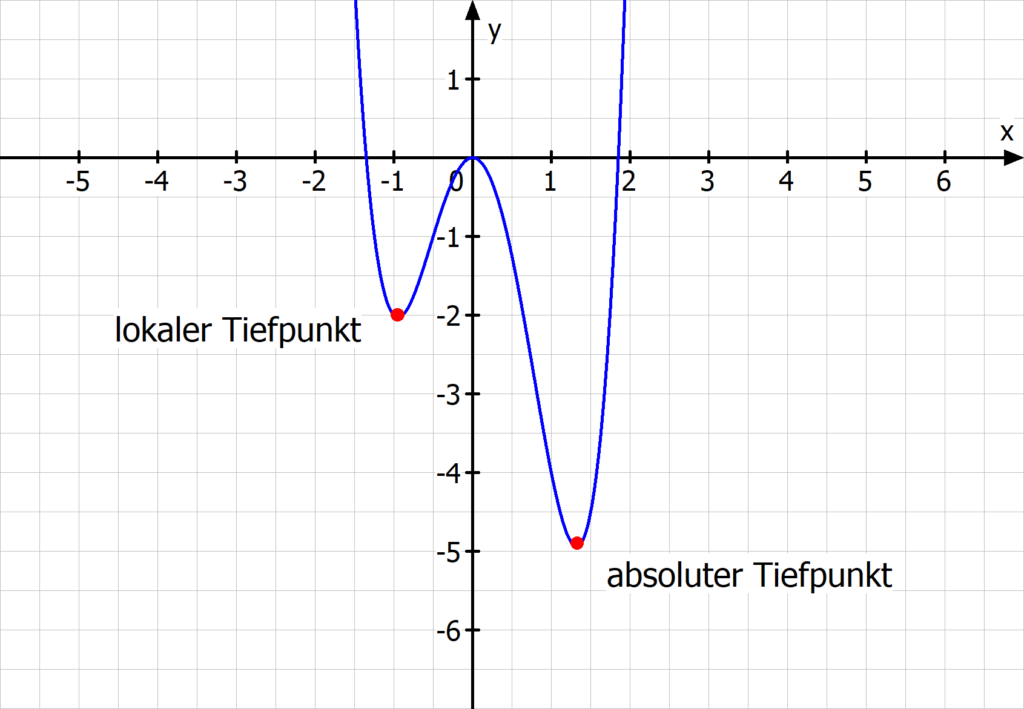
Ist das der Fall, nennst du ihn lokalen Tiefpunkt. Falls es sogar der aller tiefste Punkt deines Graphen ist, wäre das der absolute Tiefpunkt.
Jetzt musst du dir nur noch einen Sonderfall anschauen:
Spezialfall: Sattelpunkt
Es kann passieren, dass deine Ableitung an einer Stelle Null ist, es sich aber um keine Extremstelle handelt! Das ist dann ein Sattelpunkt. Dort verändert der Graph sein Monotonieverhalten nicht. Damit ist er dann weder der höchste noch der niedrigste Punkt im Graphen. Zum Beispiel steigt hier dein Graph bis er kurz stagniert und wieder weiter steigt.
Das liegt genau dann vor, wenn gilt:
- f'(x) = 0
- f“(x) = 0
Merke: Ein Sattelpunkt ist kein Extrempunkt.
Jetzt kannst du dir noch kurz anschauen, wie du Extremstellen berechnen kannst.
Extremstellen berechnen
Hier hast du eine kurze Anleitung, wie du bei einem Graphen die Extremstellen bestimmen kannst:
- Setze die Ableitung gleich Null : f'(x) = 0
-
Art der Extremstelle bestimmen. Schau dir dazu die zweite Ableitung an: f“(x) < 0 ⇒ Hochpunkt oder f“(x) > 0 ⇒ Tiefpunkt.
Schau dir dazu mal folgendes Beispiel an:
f(x) = x2 – 2x
Möchtest du hier die Extremstellen bestimmen, leitest du zuerst f ab und setzt die Ableitung gleich Null.
1. Setze die Ableitung gleich Null:
f'(x) = 2x – 2
2x – 2 = 0
xs = 1
Jetzt musst du nur noch die zweite Ableitung bilden und schauen, ob diese bei 1 größer oder kleiner als Null ist.
2. Art der Extremstelle bestimmen:
f“(x) = 2
f“(1) = 2 > 0 ⇒ Tiefpunkt
Du hast also bei deiner Extremstelle xs = 1 einen Tiefpunkt.
Extremstellen — häufigste Fragen
(ausklappen)
Extremstellen — häufigste Fragen
(ausklappen)-
Wie finde ich Extremstellen bei Funktionen mit einem Definitionsbereich?Extremstellen findest du, indem du
löst und zusätzlich Randpunkte des Definitionsbereichs prüfst. Innerhalb des Bereichs liefern die Lösungen von Kandidaten, die du mit 
als Hoch- oder Tiefpunkt einordnest. An den Rändern kann ebenfalls ein absolutes Maximum oder Minimum liegen.
-
Was mache ich, wenn die zweite Ableitung an der Stelle null ist?Wenn
ist, entscheidet der zweite-Ableitungstest nicht, ob ein Extrempunkt vorliegt. Dann prüfst du das Vorzeichen von 
links und rechts von 
: Wechsel von 
nach 
bedeutet Hochpunkt, von nach bedeutet Tiefpunkt. Bleibt das Vorzeichen gleich, liegt kein Extrempunkt vor.
-
Wie prüfe ich mit Vorzeichenwechsel, ob es ein Hochpunkt ist?Ein Hochpunkt liegt vor, wenn beim Durchgang durch von positiv zu negativ wechselt. Positiv heißt: der Graph steigt, negativ heißt: der Graph fällt. Beispiel: Gilt links von
und rechts 
, dann steigt die Funktion erst und fällt danach.
-
Welche Fehler passieren oft, wenn ich f'(x) gleich null setze?Häufige Fehler sind falsches Ableiten und das Verlieren von Lösungen beim Umformen von. Außerdem werden Kandidaten oft nicht geprüft, obwohl
auch bei einem Sattelpunkt möglich ist. Beispiel: Aus 
müssen beide Lösungen 
und 
übernommen werden.
-
Wie unterscheide ich einen Sattelpunkt von einem Wendepunkt?Ein Sattelpunkt ist ein Wendepunkt mit waagrechter Tangente, also zusätzlich. Ein Wendepunkt bedeutet, dass sich die Krümmung ändert, typisch erkennbar an einem Vorzeichenwechsel von . Beim Sattelpunkt bleibt das Monotonieverhalten gleich, obwohl kurz eine Steigung von 0 auftritt.
Extrempunkte berechnen
Willst du den dazugehörigen Extrempunkt berechnen , kannst du direkt unser Video dazu anschauen!
