Video

Quiz

Hier geht's zum Video „Potenzfunktionen“

Hier geht's zum Video „Stammfunktion“

Hier geht's zum Video „e-Funktion integrieren“

Hier geht's zum Video „Natürlicher Logarithmus“

Hier geht's zum Video „Partielle Integration“

Hier geht's zum Video „Integration durch Substitution“

Stammfunktion bilden

Wichtige Inhalte in diesem Video

Stammfunktion bilden — Potenzregel

Stammfunktion bilden — Faktorregel

Stammfunktion bilden — Summenregel

Stammfunktion bilden — e-Funktion

Stammfunktion bilden — Logarithmische Integration

Du möchtest wissen, wie du eine Stammfunktion bildest? Hier und in unserem Video erklären wir dir alle Regeln und zeigen dir anhand vieler Beispiele, wie du die Stammfunktionen verschiedener Funktionen bestimmst.

Inhaltsübersicht

Stammfunktion bilden einfach erklärt

Die Funktion F(x) ist eine Stammfunktion der Funktion f(x), wenn ihre Ableitung F'(x) genau wieder f(x) ist:

$F'(x) = f(x)$$

Eine Stammfunktion F(x) der Funktion f(x) bildest du also, indem du den Vorgang des Ableitens rückgängig machst. Du leitest quasi „auf“.

Um Stammfunktionen zu bilden, gibt es verschiedene Integrationsregeln . Im Folgenden stellen wir dir alle Regeln vor und zeigen dir anhand vieler Beispiele, wie du die Stammfunktionen für die verschiedenen Funktionstypen berechnest.

Stammfunktion bilden — Potenzregel

im Videozur Stelle im Video springen

Die Potenzregel ist die wichtigste der Integrationsregeln. Du wendest sie an, um die Stammfunktion einer Potenzfunktion (x mit einer Hochzahl) zu bestimmen.

Potenzregel

$F(x) = \int x^{\textcolor{orange}{n}} dx = \frac{1}{\textcolor{orange}{n}+1}x^{\textcolor{orange}{n}+1}+c$

Um die Stammfunktion F(x) von f(x) = xⁿ zu bestimmen, gehst du so vor:

1. Du erhöhst den Exponenten um 1. Beispiel: 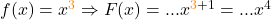$f(x) = x^{\textcolor{orange}{3}} \Rightarrow F(x) = ... x^{\textcolor{orange}{3}+1} = ... x^4$

2. Du teilst durch den neuen, um 1 erhöhten Exponenten. Beispiel: $F(x) = \frac{1}{\textcolor{blue}{4}} x^4$

Die Konstante c

Jede stetige Funktion hat nicht nur eine Stammfunktion, sondern unendlich viele. Sie unterscheiden sich immer nur durch die Konstante c, die beim Ableiten wieder wegfällt.

Ist nur nach einer Stammfunktion von f(x) gefragt, so genügt es, für c eine konkrete Zahl einzusetzen. Ist hingegen nach der Menge aller Stammfunktionen von f(x) gefragt, musst du die allgemeine Form (+ c) schreiben.

Anwendung Potenzregel — Potenzfunktionen

Mithilfe der Potenzregel kannst du die Stammfunktionen von Potenzfunktionen berechnen. Schau dir zur Veranschaulichung zwei Beispiele an:

Beispiel 1: Gesucht ist eine Stammfunktion von f(x) = x². Du suchst also eine Funktion F(x), die abgeleitet wieder f(x) = x²ergibt. Dazu berechnest du:

$F(x) = \int x^{\textcolor{orange}{n}} dx = \frac{1}{\textcolor{orange}{n}+1}x^{\textcolor{orange}{n}+1}+c$

$\Rightarrow F(x) = \int x^{\textcolor{orange}{2}} dx = \frac{1}{\textcolor{orange}{2}+1}x^{\textcolor{orange}{2}+1}+c = \frac{1}{3}x^{3}+c$

Konkrete Stammfunktionen von f(x) = x²sind beispielsweise 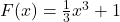$F(x) = \frac{1}{3}x^{3}+1$ (c = 1) oder $F(x) = \frac{1}{3}x^{3}-2$ (c = -2). In beiden Fällen erhältst du wieder f(x) = x², wenn du nach x ableitest.

Beispiel 2: Gesucht ist eine Stammfunktion von f(x) = 1. Auch hier kommt die Potenzregel zum Einsatz, denn die Zahl 1 kannst du auch als x⁰ schreiben. Du berechnest also:

$F(x) = \int x^{\textcolor{orange}{n}} dx = \frac{1}{\textcolor{orange}{n}+1}x^{\textcolor{orange}{n}+1}+c$

$\Rightarrow F(x) = \int x^{\textcolor{orange}{0}} dx = \frac{1}{\textcolor{orange}{0}+1}x^{\textcolor{orange}{0}+1}+c =\frac{1}{1}x^{1}+c = x+c$

Eine konkrete Stammfunktion zu f(x) = 1 wäre somit beispielsweise F(x)= x+4 (c = 4) oder F(x)= x (c = 0).

Anwendung Potenzregel — Brüche

Du kannst die Potenzregel auch anwenden, um die Stammfunktion von Brüchen zu berechnen. Hierfür musst du die Bruchfunktion lediglich in eine Potenzfunktion mit negativem Exponenten umschreiben. Schau dir dafür folgendes Beispiel an:

Gesucht ist eine Stammfunktion von $f(x) = \frac{1}{x^3}$ . Diese Funktion kannst du umschreiben als:

$f(x) = x^{-3}$

Nun kannst du zum Stammfunktion berechnen die Potenzregel anwenden:

$F(x) = \int x^{\textcolor{orange}{n}} dx = \frac{1}{\textcolor{orange}{n}+1}x^{\textcolor{orange}{n}+1}+c$

$\Rightarrow F(x) = \int x^{\textcolor{orange}{-3}} dx = \frac{1}{\textcolor{orange}{-3}+1}x^{\textcolor{orange}{-3}+1}+c = -\frac{1}{2}x^{-2}+c$

Eine Stammfunktion von $f(x) = x^{-3}$ ist beispielsweise $F(x) = -\frac{1}{2}x^{-2}+3$ (c = 3).

Vorsicht! Eine Ausnahme bildet die Funktion $f(x) = \frac{1}{x}$ . Diese Funktion kannst du wie folgt umschreiben:

$f(x) = x^{-1}$

Da du bei Anwendung der Potenzregel eine Null im Exponenten erhalten würdest, greift hier die logarithmische Integrationsregel:

$F(x) = \int \frac{\textcolor{teal}{f'(x)}}{\textcolor{purple}{f(x)}} dx = \ln|\textcolor{purple}{f(x)}|+c$

Die Stammfunktion F(x) von $f(x) = \frac{1}{x}$ berechnest du also wie folgt:

$F(x) = \int \frac{\textcolor{teal}{1}}{\textcolor{purple}{x}} dx = \ln|\textcolor{purple}{x}|+c$

Die logarithmische Integration erklären wir dir später noch etwas genauer!

Anwendung Potenzregel — Wurzeln

Auch Wurzelfunktionen lassen sich so umformen, dass du die Stammfunktion über die Potenzregel berechnen kannst. Schau dir dafür folgendes Beispiel an:

Gesucht ist eine Stammfunktion von $f(x) = \sqrt[3]{x}$ . Diese Funktion kannst du umschreiben als:

$f(x) = x^\frac{1}{3}$

Nun kannst du zum Stammfunktion berechnen wieder die Potenzregel anwenden:

$F(x) = \int x^{\textcolor{orange}{n}} dx = \frac{1}{\textcolor{orange}{n}+1}x^{\textcolor{orange}{n}+1}+c$

$\Rightarrow F(x) = \int x^{\textcolor{orange}{\frac{1}{3}}} dx = \frac{1}{{\textcolor{orange}{\frac{1}{3}}}+1} x^{{\textcolor{orange}{\frac{1}{3}}}+1}+c= \frac{3}{4}x^{\frac{4}{3}}+c$

Eine konkrete Stammfunktion F(x) von 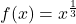$f(x) = x^\frac{1}{3}$ ist also beispielsweise $F(x)= \frac{3}{4}x^{\frac{4}{3}}-5$ (c = -5).

Stammfunktion bilden — Faktorregel

im Videozur Stelle im Video springen

Die Faktorregel ist eine der einfachsten Integrationsregeln. Du benutzt sie, wenn die Funktion, deren Stammfunktion du bilden möchtest, einen konstanten Faktor a enthält.

Faktorregel

$F(x) = \int \textcolor{teal}{a} \cdot f(x) dx= \textcolor{teal}{a} \cdot \int f(x)dx$

Beim Bilden der Stammfunktion kannst du den Faktor a vor das Integralzeichen ziehen und sozusagen „ausklammern “.

Schau dir dafür ein Beispiel an:

Gesucht ist die Stammfunktion von $f(x) = \textcolor{teal}{2}x^2$ . Diese berechnest du wie folgt:

$F(x) = \int \textcolor{teal}{2}x^2dx = \textcolor{teal}{2} \cdot \int x^2 dx = \textcolor{teal}{2} \cdot \frac{1}{3}x^3 + c = \frac{2}{3}x^3 +c$

Stammfunktion bilden — Summenregel

im Videozur Stelle im Video springen

Die Summenregel kommt immer dann zum Einsatz, wenn die Funktion, deren Stammfunktion du suchst, eine Summe enthält.

Summenregel

$F(x) = \int (\textcolor{olive}{f(x)}+\textcolor{magenta}{g(x)}) dx = \int \textcolor{olive}{f(x)} dx + \int \textcolor{magenta}{g(x)} dx$

Beim Stammfunktion berechnen kannst du die einzelnen Summanden einer Summe „auseinanderziehen“ und einzeln integrieren .

Schau dir dafür folgendes Beispiel an:

Gesucht ist die Stammfunktion F(x) von $f(x) = \textcolor{olive}{x^3}+\textcolor{magenta}{x^5}$ . Diese berechnest du wie folgt:

$F(x) = \int \textcolor{olive}{x^3}+\textcolor{magenta}{x^5} dx = \int \textcolor{olive}{x^3} dx + \int \textcolor{magenta}{x^5} dx = \textcolor{olive}{\frac{1}{4}x^4}+\textcolor{magenta}{\frac{1}{6}x^6}+c$

Stammfunktion bilden — Differenzregel

Analog zur Summenregel kommt die Differenzregel immer dann zum Einsatz, wenn die Funktion, deren Stammfunktion du suchst, eine Differenz enthält.

Differenzregel

$F(x) = \int (\textcolor{olive}{f(x)} - \textcolor{magenta}{g(x)}) dx = \int \textcolor{olive}{f(x)} dx - \int \textcolor{magenta}{g(x)} dx$

Beim Stammfunktion berechnen kannst du die Differenz „auseinanderziehen“ und die einzelnen Bestandteile einzeln integrieren.

Schau dir dafür folgendes Beispiel an:

Gesucht ist die Stammfunktion F(x) von $f(x) = \textcolor{olive}{4x}-\textcolor{magenta}{x^6}$ . Diese berechnest du wie folgt:

$F(x) = \int \textcolor{olive}{4x} - \textcolor{magenta}{x^6} dx = \int \textcolor{olive}{4x} dx - \int \textcolor{magenta}{x^6}dx = \textcolor{olive}{2x^2} - \textcolor{magenta}{\frac{1}{7}x^7}+c$

Stammfunktion bilden — e-Funktion

im Videozur Stelle im Video springen

Da die Ableitung von e^xwieder e^x ist, lautet die Stammfunktion der e-Funktion ganz einfach:

Stammfunktion e-Funktion

$F(x) = \int e^x dx = e^x+c$

Steht in der Potenz der e-Funktion noch ein Faktor b, bildest du die Stammfunktion wie folgt:

Stammfunktion spezielle e-Funktion

$F(x) = \int e^{\textcolor{purple}{b} x} dx = \frac{1}{\textcolor{purple}{b}} e^{\textcolor{purple}{b} x}+c$

Beispiel: Gesucht ist die Stammfunktion F(x) von $f(x) = e^{\textcolor{purple}{3} x}$ . Diese bildest du wie folgt:

$F(x) = \int e^{\textcolor{purple}{3} x} dx = \frac{1}{\textcolor{purple}{3}} e^{\textcolor{purple}{3} x}+c$

Wenn du es mit noch komplizierteren Funktionen zu tun hast, dann schau dir unser Video speziell zum Integrieren von e-Funktionen an.

Stammfunktion bilden — Partielle Integration

Du wendest die partielle Integration an, um die Stammfunktion von einem Produkt von Funktionen zu bestimmen. Du nennst die partielle Integration daher auch Produktintegration.

Partielle Integration

$F(x) = \int \textcolor{red}{f'(x)} \cdot \textcolor{blue}{g(x)} dx = \textcolor{red}{f(x)} \cdot \textcolor{blue}{g(x)} -\int \textcolor{red}{f(x)}\cdot \textcolor{blue}{g'(x)} dx$

Am besten verstehst du die partielle Integration an einem Beispiel:

Gesucht ist die Stammfunktion F(x) von:

$f(x) = e^x \cdot x$

Um F(x) zu bestimmen, gehst du wie folgt vor:

Zuerst entscheidest du, welche Funktion dein f'(x) und welche dein g(x) sein soll. Die Funktion, die sich durch das Ableiten vereinfacht, wird dein g(x). e^xvereinfacht sich durch Ableiten nicht, da e^xabgeleitet wieder e^xergibt. x wird durch Ableiten vereinfacht, denn es wird zu 1. Damit ist g(x) = x und f'(x) = e^x.

Jetzt stellst du f(x) und g'(x) auf:

$\textcolor{red}{f'(x) = e^x} \qquad \underrightarrow{integrieren} \qquad \textcolor{red}{f(x) = e^x}$

$\textcolor{blue}{g(x) = x} \qquad \underrightarrow{ableiten} \qquad \textcolor{blue}{g'(x) = 1}$

Setze deine Ergebnisse in die Formel ein:

$F(x) = \int \textcolor{red}{f'(x)} \cdot \textcolor{blue}{g(x)} dx &= \textcolor{red}{f(x)} \cdot \textcolor{blue}{g(x)} -\int \textcolor{red}{f(x)}\cdot \textcolor{blue}{g'(x)} dx$

$\begin{align*} \Rightarrow F(x) = \int \textcolor{red}{e^x} \cdot \textcolor{blue}{x} dx &= \textcolor{red}{e^x} \cdot \textcolor{blue}{x} -\int \textcolor{red}{e^x}\cdot \textcolor{blue}{1} dx \\ &= \textcolor{red}{e^x} \cdot \textcolor{blue}{x} - \int \textcolor{red}{e^x} dx \\ &= e^x \cdot x - e^x +c \\ &= e^x(x-1) +c\end{align*}$

Stammfunktion bilden — ln(x)

Jetzt, wo du die partielle Integration kennst, kannst du dir auch die Stammfunktion von ln(x) herleiten:

$F(x) = \int \textcolor{red}{f'(x)} \cdot \textcolor{blue}{g(x)} dx = \textcolor{red}{f(x)} \cdot \textcolor{blue}{g(x)} -\int \textcolor{red}{f(x)}\cdot \textcolor{blue}{g'(x)} dx$

$\Rightarrow F(x) = \int \textcolor{blue}{\ln(x)} dx = \int \textcolor{red}{1}\cdot \textcolor{blue}{\ln(x)} dx = \textcolor{red}{x} \cdot \textcolor{blue}{\ln(x)} -\int \textcolor{red}{x} \cdot \textcolor{blue}{\frac{1}{x}} dx = \textcolor{red}{x} \cdot \textcolor{blue}{\ln(x)}-\int 1 dx= x\cdot \ln(x)-x+c$

Die Stammfunktion von ln(x) lautet demnach:

Stammfunktion ln(x)

$F(x) = \int \ln(x) dx = x\cdot \ln(x)-x+c$

Stammfunktion bilden — Logarithmische Integration

im Videozur Stelle im Video springen

Wie wir dir oben bereits gezeigt haben, lautet die Stammfunktion von $f(x) = \frac{1}{x}$ wie folgt:

$F(x) = \int \frac{1}{x} dx = \ln|x|+c$

Dies ist ein Spezialfall der logarithmischen Integration. Du wendest sie an, wenn du die Stammfunktion eines Bruches suchst, bei dem der Zähler die Ableitung des Nenners ist. Die Stammfunktion bestimmst du dann mit dem natürlichen Logarithmus ln des Nenners:

Logarithmische Integration

$F(x) = \int \frac{\textcolor{teal}{f'(x)}}{\textcolor{purple}{f(x)}} dx = \ln|\textcolor{purple}{f(x)}|+c$

Schau dir zum besseren Verständnis folgendes Beispiel an:

Gesucht ist die Stammfunktion von:

$f(x) = \frac{\textcolor{teal}{3x^2+2x}}{\textcolor{purple}{x^3+x^2}}$

Wenn du genau hinschaust, erkennst du, dass der Zähler $\textcolor{teal}{3x^2+2x}$ die Ableitung des Nenners $\textcolor{purple}{x^3+x^2}$ ist. Die Stammfunktion F(x) lautet daher:

$F(x) = \int \frac{\textcolor{teal}{3x^2+2x}}{\textcolor{purple}{x^3+x^2}} dx = \ln|\textcolor{purple}{x^3+x^2}|+c$

Integration durch Substitution

Die Integration durch Substitution wendest du an, um verkettete Funktionen zu integrieren. Verkettet heißt, dass es eine äußere und eine innere Funktion gibt.

Die Substitutionsregel ist im Vergleich zu den bisher vorgestellten Integrationsregeln etwas komplizierter. Wir haben dir daher ein eigenes Video vorbereitet, in dem wir dir alles Wichtige rund um die Integration durch Substitution anhand vieler Beispiele erklären!

Hier stellen wir dir nur kurz die Formel und ein typisches Beispiel vor.

Substitutionsregel

$\int\limits_a^b \textcolor{teal}{f(}\textcolor{orange}{\varphi(t)}\textcolor{teal}{)}\cdot \textcolor{orange}{\varphi '(t)}\mathrm{d}t=\int\limits_{\varphi(a)}^{\varphi(b)}f(x)\mathrm{d}x$

Die Substitutionsregel brauchst du zum Beispiel, um die Funktion $f(x)=\textcolor{teal}{\sin(}\textcolor{orange}{2x}\textcolor{teal}{)}$ zu integrieren. Hierbei handelt es sich um eine verkettete Funktion, wobei $\textcolor{teal}{sin( )}$ die äußere Funktion und $\textcolor{orange}{2x}$ die innere Funktion darstellt.

Stammfunktion bilden — Sinus und Cosinus

Die Stammfunktion von Sinus und Cosinus bestimmst du am leichtesten mit Blick auf die Ableitung.

Für die Ableitung gilt:

$\textcolor{olive}{f(x) = \sin(x)} \quad \Longleftrightarrow \quad \textcolor{olive}{f'(x) = \cos(x)}$

$\textcolor{magenta}{f(x) = \cos(x)} \quad \Longleftrightarrow \quad \textcolor{magenta}{f'(x) = -\sin(x)}.$

Damit gilt für die Integration:

$\textcolor{magenta}{F(x) = \int \sin(x) dx = -\cos(x)+c}$

$\textcolor{olive}{F(x) = \int \cos(x) dx = \sin(x)+c}.$

Übersicht Stammfunktion bilden — Regeln

Prima! Du kennst jetzt alle Regeln, die du fürs Stammfunktion bilden brauchst. Hier haben wir dir die wichtigsten Integrationsregeln nochmal in einer Tabelle zusammengefasst:

Regel	Formel
Potenzregel	$F(x) = \int x^n dx = \frac{1}{n+1}x^{n+1}+c$
Faktorregel	$F(x) = \int a \cdot f(x) dx= a \cdot \int f(x)dx$
Summenregel	$F(x) = \int (f(x)+g(x)) dx = \int f(x) dx + \int g(x) dx$
Differenzregel	$F(x) = \int (f(x)- g(x)) dx = \int f(x) dx - \int g(x) dx$
Partielle Integration	$F(x) = \int f'(x) \cdot {g(x) dx = f(x) \cdot g(x) -\int f(x) \cdot g'(x) dx$
Logarithmische Integration	$F(x) = \int \frac{f'(x)}{f(x)} dx = \ln\|f(x)\|+c$

Partielle Integration

Geschafft! Jetzt weißt du, wie du die Stammfunktion für verschiedene Funktionstypen bestimmst. Dabei helfen dir die Integrationsregeln wie etwa die partielle Integration. Du möchtest das Verfahren der partiellen Integration anhand mehrerer Beispiele noch weiter vertiefen? Dann schau dir unser Video dazu an!

Zum Video: Partielle Integration

zur Videoseite: Stammfunktion bilden

Beliebte Inhalte aus dem Bereich Analysis

Integralrechnung einfach erklärt

Stammfunktion bilden

Integrationsregeln

Integralrechnung

Hauptsatz der Differential- und Integralrechnung

Integralfunktion

Thema präsentiert von unserem Werbepartner

Zur Webseite

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Bitte .