Stammfunktion
Du möchtest wissen, was es mit dem Begriff Stammfunktion auf sich hat? Wie du sie für die verschiedenen Funktionen berechnest, erklären wir dir hier anschaulich und mit vielen Beispielen.
Du lernst leichter, wenn es dir jemand direkt erklärt und du keinen Text durcharbeiten musst? Dann schau dir einfach unser Video zum Thema Stammfunktion an!
Inhaltsübersicht
Stammfunktion einfach erklärt
Eine Stammfunktion berechnen, ist ein zentraler Aspekt der Integralrechnung . Sie hängt eng mit dem unbestimmten Integral zusammen und ist wie folgt definiert:
Sei 
die Stammfunktion einer reellen Funktion 
. Dann ist ihre Ableitung 
gerade wieder .
Sie ist deswegen sehr wichtig, weil man in der Praxis oft nur die Ableitung einer Funktion (also die Änderungsrate) kennt und daraus auf die ursprüngliche Funktion schließen möchte.
Merke: Klassischerweise verwendet man für die Stammfunktion immer Großbuchstaben.
Sehr praktisch ist, dass jede stetige Funktion eine Stammfunktion besitzt! Du musst also nur noch wissen, wie man sie findet. Das erklären wir dir im nächsten Abschnitt.
Stammfunktion bilden
Angenommen, du möchtest eine Stammfunktion F(x) von f(x) berechnen
und du weißt bereits, dass dann gelten muss. Es wäre also kein Problem, ausgehend von durch Ableiten zu bestimmen. Wir wollen diesen Vorgang jetzt rückgängig machen, d.h. statt Ableiten wollen wir Aufleiten. Formal heißt das in der Mathematik „integrieren“, die entsprechende Notation dazu lautet
Um Integrale zu berechnen, gibt es verschiedene Integrationsregeln
, die wir dir in einem separaten Video zusammengefasst haben. Im Wesentlichen überlegst du dir dabei immer, wie aussehen muss, damit es abgeleitet ergibt.
Manchmal spricht man statt von Stammfunktionen auch von der Aufleitung. Versuch das am besten zu vermeiden, es ist sehr umgangssprachlich.
Merke: Jede stetige Funktion hat nicht nur eine Stammfunktion, sondern unendlich viele. Sie unterscheiden sich jedoch immer nur durch die Konstante 
, die addiert oder subtrahiert wird, und die beim Ableiten wieder wegfällt.
Wenn also allgemein nach Stammfunktionen gefragt wird, vergiss am Ende die Konstante nicht. Man sagt auch, dass du in diesem Falle ein unbestimmtes Integral berechnest.
Stammfunktion Potenzfunktionen
Die Stammfunktion von Potenzfunktionen 
lässt sich sehr einfach berechnen als 
. Das wollen wir an einem kurzen Beispiel veranschaulichen:
-
Beispiel 1: Gesucht ist eine Stammfunktion von
. Wir suchen also eine Funktion , die abgeleitet gerade ergibt. Dazu berechnen wir
Nun müssen wir uns überlegen, was abgeleitet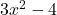 
ergeben würden und sehen sofort (unter Berücksichtigung der Ableitungsregeln
), dass
Allerdings ergeben auch 
und 
abgeleitet die ursprüngliche Funktion . Die allgemeine Stammfunktion lautet daher 
, mit der Konstanten .
Stammfunktion Bruch und Stammfunktion 1/x
Für Brüche funktioniert das analog, wenn du sie in eine Potenzfunktion mit negativem Exponenten umschreibst:
Das funktioniert auch für andere Brüche, die zum Beispiel keine 1 im Zähler haben. Wie genau siehst du im nächsten Beispiel.
-
Beispiel 2: Gesucht ist die Stammfunktion von
. Diesen Ausdruck kannst du umschreiben als
Die rechte Seite lässt sich nun leicht integrieren.
Eine Ausnahme bildet die Stammfunktion 1/x, was du sofort siehst, wenn du sie wie oben umschreibst.
Weil du hier mit der klassischen Regel eine Null im Exponenten erhalten würdest – was offensichtlich falsch ist – greift hier die logarithmische Integrationsregel, die besagt, dass
In unserem Fall ist das Integral von 
daher
Stammfunktion Wurzel
Auch Wurzeln kannst du im obigen Sinne umschreiben und sie dadurch leichter integrieren. Es ist
und damit gilt für die Stammfunktion
Analog klappt das auch für die zweite, dritte oder n-te Wurzel, wie du im nächsten Beispiel siehst.
-
Beispiel 3: Wir wollen
![f(x) = \sqrt[5]{x^3}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-35a71023cae0e4d4e0d3e87f95e2d304_l3.png "Rendered by QuickLaTeX.com")
integrieren. Dieser Ausdruck lässt sich umschreiben als
![\sqrt[5]{x^3} = x^\frac{3}{5}.](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-bd51bcbadc029f609980b9797e176394_l3.png "Rendered by QuickLaTeX.com")
Damit lässt sich das Integral berechnen
![\int \sqrt[5]{x^3} dx = \int x^\frac{3}{5} dx = \frac{5}{8} x^\frac{8}{5} = \frac{5}{8} \sqrt[5]{x^8} .](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-743035b9d8f0420de998ac4331fe866c_l3.png "Rendered by QuickLaTeX.com")
Stammfunktion ln(x) und e Funktion
Die e-Funktion lässt sich sehr einfach integrieren, wenn du weißt, dass von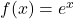 
die Ableitung wieder 
ist. Damit gilt:
Die Stammfunktion lnx ist etwas schwieriger. Sie lautet
Dass dieses Integral so kompliziert ist, liegt daran, dass man es nur mit partieller Integration berechnen kann. Es gilt
![\int \ln(x) dx = \int 1\cdot \ln(x) dx = \biggl[x\cdot \ln(x)\biggr]-\int x \cdot \frac{1}{x} dx = \biggl[x\cdot \ln(x)\biggr]-\int 1 dx= x\cdot \ln(x)-x+c.](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0ea4c2698282847f0f5cb26c4dbedaca_l3.png "Rendered by QuickLaTeX.com")
Stammfunktionen sin(x) und cos(x)
Das Integral von Sinus und Cosinus bestimmst du am leichtesten mit Blick auf die Ableitung. Du weißt bereits, dass
Damit ist klar, dass gilt
Zusammenhang zur Ableitung
Integrieren und Differenzieren – wie Ableiten in der Fachsprache heißt – hängen also eng zusammen. Das besagt der sogenannte HDI, der Hauptsatz der Differential- und Integralrechnung , der dir ermöglicht, Stammfunktionen wie im obigen Beispiel zu berechnen. Im Allgemeinen kannst du dir den Zusammenhang wie im Bild vorstellen.
Stammfunktion Tabelle
Alle Ergebnisse haben wir dir noch einmal übersichtlich in dieser Tabelle zusammengefasst.
| Funktion f(x) | Stammfunktion F(x) |
| 1 | x + c |
| xn |  |
|
ln(|x|) + c |
 |
 |
| sin(x) | -cos(x) + c |
| cos(x) | sin(x) + c |
| ex | ex + c |
| ln(x) | x • ln(x) – x + c |
| ax |  |
Bestimmtes und unbestimmtes Integral
Super, du weißt jetzt was eine Stammfunktion ist! Die brauchst du unbedingt, um Integrale berechnen zu können. Wie du dabei vorgehst und was die Unterschiede zwischen einem bestimmten und einem unbestimmten Integral sind, erfährst du in unserem Video dazu. Schau es dir unbedingt gleich an!
