Bruchterme
Du fragst dich, was Bruchterme sind und wie du mit ihnen rechnest? Das und worauf du besonders achten musst, erklären wir dir hier und im Video !
Inhaltsübersicht
Was sind Bruchterme?
Ein Bruchterm ist wie ein normaler Bruch, der zusätzlich mindestens eine Variable im Nenner enthält. Bruchterme haben ebenfalls einen Zähler und Nenner.
Zum Beispiel ist  ein einfacher Bruch, während
ein einfacher Bruch, während  ein Bruchterm ist. Aber Achtung, der Nenner eines Bruchs darf niemals null sein, da du nicht durch null teilen kannst. Deshalb musst du bei Bruchtermen immer die Definitionsmenge bestimmen.
ein Bruchterm ist. Aber Achtung, der Nenner eines Bruchs darf niemals null sein, da du nicht durch null teilen kannst. Deshalb musst du bei Bruchtermen immer die Definitionsmenge bestimmen.
Die Definitionsmenge gibt an, für welche Werte der Variablen der Bruchterm gültig ist.
Sie schließt alle Werte aus, die den Nenner null machen würden.
Dadurch würde der Bruch nämlich ungültig werden!
Beispiel:
![Rendered by QuickLaTeX.com \[\frac{1}{x - 2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0771301084f8af138b3853c781095f8a_l3.png)
Der Nenner wird Null, wenn
x – 2 = 0 | +2
x = 2 ist.
Du musst also in der Definitionsmenge die 2 ausschließen.
Das schreibst du so D =  \ {2}
\ {2}
Bruchterme kürzen
Du kürzt Bruchterme, indem du den Zähler und den Nenner durch dieselbe Zahl teilst.
Beispiel:
![Rendered by QuickLaTeX.com \[\frac{(x - 1)(x + 2)}{x(x - 1)}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-27db0f5391c7ccc57227958f5e095007_l3.png)
-
Schaue dir den Zähler und den Nenner an.
(x – 1) (x + 2) und x (x – 1)
- Finde gemeinsame Faktoren im Zähler und Nenner.
(x – 1) (x + 2) und x (x – 1)
-
Nun kannst du den Faktor (x – 1) im Zähler und Nenner streichen.
![Rendered by QuickLaTeX.com \[\frac{\cancel{(x - 1)}(x + 2)}{x\cancel{(x - 1)}} = \frac{x + 2}{x}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5a71e7b7887c0bfd4fcba6d8ae62fbfb_l3.png)
- Die Definitionsmenge vor dem Kürzen des Bruchterms ist
D =
Sie setzt sich folgendermaßen zusammen:
x (x – 1) = 0 | Der Nenner wird 0, wenn eines der beiden x eine 0 erzeugt.
Wenn x = 0, wird der Nenner zu 0 ⋅ (0 – 1) = 0 ⋅ (-1) = 0
Wenn x = 1, wird der Nenner zu 1 ⋅ (1 – 1) = 1 ⋅ 0 = 0
-
Wichtig: Nach dem Kürzen ändert sich die Definitionsmenge, wenn du einen Term komplett aus dem Nenner entfernst, mit dem er eigentlich 0 wird.
Hier kann x mit 1 nicht mehr 0 werden, also heißt unsere Definitionsmenge jetzt: D =
D = 
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Bruchterme erweitern
Du erweiterst Bruchterme, indem du den Zähler und den Nenner mit derselben Zahl multiplizierst.
Übrigens: Der Wert des Bruchterms wird dabei nicht verändert.
Beispiel:
![Rendered by QuickLaTeX.com \[\frac{2}{x + 1}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f14a1d14c9813e1f6e6848eeca6c19d1_l3.png)
mit (x – 1) erweitern
-
Schaue dir den Zähler und den Nenner an.
2 und (x + 1) -
Multipliziere Zähler und Nenner mit (x – 1).
![Rendered by QuickLaTeX.com \[\frac{2}{x + 1} \cdot \frac{x - 1}{x - 1} = \frac{2(x - 1)}{(x + 1)(x - 1)}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-de39e1ab3ffaec2ab3fdfec550f6d2d9_l3.png)
Definitionsmenge:
- Die Definitionsmenge vor dem Erweitern des Bruchterms ist
D =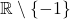
-
Wichtig: Nach dem Erweitern musst du die Definitionsmenge neu bestimmen:
Wenn x = -1, wird der Nenner zu (-1 + 1)(-1 – 1) = 0 ⋅ (-2) = 0
Wenn x = 1, wird der Nenner zu (1 + 1)(1 – 1) = 2 ⋅ 0 = 0
Also ist jetzt D =
Hauptnenner von Bruchtermen bilden
Damit du Bruchterme addieren oder subtrahieren kannst, müssen sie den gleichen Nenner haben. Der kleinste gemeinsame Nenner wird auch Hauptnenner genannt. Um Bruchterme auf denselben Nenner zu bringen, kannst du so vorgehen:
Beispiel:
![Rendered by QuickLaTeX.com \[\frac{3}{x} + \frac{1}{x + 2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8a199ee8fcade591a8e26f14eeae515b_l3.png)
-
Schaue dir die Nenner an.
x und (x + 2) -
Finde den Hauptnenner:
Er ist das Produkt der verschiedenen Nenner.
x ⋅ (x + 2) -
Bringe beide Bruchterme auf den Hauptnenner:
-
Erweitere den ersten Bruchterm mit (x + 2).
![Rendered by QuickLaTeX.com \[\frac{3}{x} \cdot \frac{x+2}{x+2} = \frac{3(x + 2)}{x(x + 2)} = \frac{3x + 6}{x(x + 2)}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8fbe8c21fce94d4db8c57e45a7b4384a_l3.png)
-
Erweitere den zweiten Bruchterm mit x.
![Rendered by QuickLaTeX.com \[\frac{1}{x + 2} \cdot \frac{x}{x} = \frac{x}{x(x + 2)}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d5b56bdd89dbcc8e84a9ef121af8215a_l3.png)
-
Jetzt kannst du mit den beiden Bruchtermen weiter rechnen.
Definitionsmenge:
Wichtig: Durch das Erweitern der Bruchterme auf einen Hauptnenner verschmelzen die jeweiligen Definitionsmengen.
-
 mit D =
mit D = 
-
 mit D =
mit D = 
werden zu
-
 mit D =
mit D = 
-
 mit D =
mit D = 
Bruchterme addieren
Um Bruchterme zu addieren, musst du sie zuerst auf einen gemeinsamen Nenner bringen. Erst danach kannst du die Zähler addieren.
Beispiel:
![Rendered by QuickLaTeX.com \[\frac{1}{x - 4} + \frac{x + 1}{x}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-45daf1a88d8b6d33a0593e524b971996_l3.png)
-
Bringe beide Bruchterme auf den Hauptnenner
x ⋅ (x−4)-
Erweitere den ersten Bruchterm mit x.
![Rendered by QuickLaTeX.com \[\frac{1}{x-4} \cdot \frac{x}{x} = \frac{x}{x(x - 4)}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-330063a3d45cf48554e75b1582f7e688_l3.png)
-
Erweitere den zweiten Bruchterm mit (x – 4).
![Rendered by QuickLaTeX.com \[\frac{x+1}{x} \cdot \frac{x-4}{x-4} = \frac{(x+1)(x-4)}{x(x - 4)} = \frac{x^2 - 3x - 4}{x(x - 4)}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8378f002dcad939b4e7ecce022592cdb_l3.png)
-
-
Addiere die Zähler der beiden Bruchterme.
![Rendered by QuickLaTeX.com \[\frac{x}{x(x - 4)} + \frac{x^2 - 3x - 4}{x(x - 4)} = \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f9df3b0575244e56ab515744602215a3_l3.png)
![Rendered by QuickLaTeX.com \[\frac{x + (x^2 - 3x - 4)}{x(x - 4)} = \frac{x^2 - 2x - 4}{x(x - 4)}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1924d4dedf0501abbb016d3084524d61_l3.png)
Definitionsmenge:
-
Die Definitionsmengen der ursprünglichen Bruchterme sind:
 mit D =
mit D = 
 mit D =
mit D = 
-
Wichtig: Die Definitionsmenge nach dem Addieren setzt sich aus den Definitionsmengen der ursprünglichen Bruchterme zusammen.
Die neue Definitionsmenge ist also D =
Bruchterme subtrahieren
Um Bruchterme zu subtrahieren, musst du sie ebenfalls zuerst auf einen gemeinsamen Nenner bringen. Danach kannst du die Zähler subtrahieren.
Beispiel:
![Rendered by QuickLaTeX.com \[\frac{3x}{x + 2} - \frac{1}{(x + 2)^2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b6ab145f0f4a45bd7697c99fe4ed2873_l3.png)
-
Bringe beide Bruchterme auf den Hauptnenner
(x + 2)2-
Erweitere den ersten Bruchterm mit (x+2).
![Rendered by QuickLaTeX.com \[\frac{3x}{x + 2} \cdot \frac{x + 2}{x + 2} = \frac{3x(x + 2)}{(x + 2)^2} =\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-fe59f02c342afc8f7c80781219e15246_l3.png)
![Rendered by QuickLaTeX.com \[\frac{3x^2 + 6x}{(x + 2)^2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-e30d6d759ee6dfa0c7726875b9e0efb2_l3.png)
-
Der zweite Bruchterm bleibt in diesem Beispiel unverändert.
Das kommt daher, dass der Nenner hier schon gleich dem Hauptnenner ist.
![Rendered by QuickLaTeX.com \[\frac{1}{(x + 2)^2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b62d39ee2dd7de1f3353c23b0700111a_l3.png)
-
-
Subtrahiere die Zähler der beiden Bruchterme.
![Rendered by QuickLaTeX.com \[\frac{3x^2 + 6x}{(x + 2)^2} - \frac{1}{(x + 2)^2} = \frac{3x^2 + 6x - 1}{(x + 2)^2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-6fa99d2623567a3b6970a0f0d3343afb_l3.png)
Definitionsmenge:
-
Die Definitionsmengen der ursprünglichen Bruchterme sind:
 mit D =
mit D = 
 mit D =
mit D = 
-
Wichtig: Die Definitionsmenge nach dem Subtrahieren setzt sich wieder aus denen der ursprünglichen Bruchterme zusammen.
Hier stimmen sie bereits überein. D bleibt also
Bruchterme multiplizieren
Um Bruchterme zu multiplizieren, nimmst du die Zähler und die Nenner mal.
Beispiel:
![Rendered by QuickLaTeX.com \[\frac{10}{x - 5} \cdot \frac{x}{x + 2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d85e1da1811a1d32b62b8317b1c8f03d_l3.png)
-
Multipliziere die Zähler.
10 ⋅ x = 10x -
Multipliziere die Nenner.
(x − 5) ⋅ (x + 2) = (x − 5)(x + 2) -
Schreibe das Ergebnis als neuen Bruch.
![Rendered by QuickLaTeX.com \[\frac{10x}{(x - 5)(x + 2)}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-6be78bc425b9d956ebd6c61e265dfb16_l3.png)
Definitionsmenge:
-
Die Definitionsmengen der ursprünglichen Bruchterme sind:
 mit D =
mit D = 
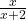 mit D =
mit D = 
-
Wichtig: Die Definitionsmenge nach dem Multiplizieren schließt alle Nullstellen der ursprünglichen Bruchterme aus.
Die neue Definitionsmenge ist also D =
Bruchterme dividieren
Um Bruchterme zu dividieren, nimmst du den ersten Bruchterm mit dem Kehrwert des zweiten Bruchterms mal. Den Kehrwert eines Bruchterms bildest du, indem du seinen Zähler und Nenner einfach vertauscht.
Beispiel:
![Rendered by QuickLaTeX.com \[\frac{1}{x - 12} \div \frac{x + 1}{5 - x}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3c63e5e07e1df5d65724e114653fdcd6_l3.png)
-
Schreibe die Division als Multiplikation mit dem Kehrwert.
![Rendered by QuickLaTeX.com \[\frac{1}{x - 12} \cdot \frac{5 - x}{x + 1}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-39b8f9bc47ea548b24944f8fcb45b9df_l3.png)
-
Vereinfache den Ausdruck.
![Rendered by QuickLaTeX.com \[\frac{1 \cdot (5 - x)}{(x - 12) \cdot (x + 1)}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-71cb4350daafb11520a81ada268469cc_l3.png)
Definitionsmenge:
-
Die Definitionsmengen der ursprünglichen Bruchterme sind:
 mit D =
mit D = 
 mit D =
mit D = 
-
Wichtig: Nach dem Dividieren werden die Definitionsmenge der ursprünglichen Bruchterme zusammengefasst.
Sie wird zu D =
Übungen zu Bruchtermen
Hier sind einige Übungen, die du machen kannst, um im rechnen mit Bruchtermen sicherer zu werden.
Gib jeweils das Ergebnis und die Definitionsmenge an.
-
Kürze den Bruchterm:
![Rendered by QuickLaTeX.com \[\frac{2x^2}{4x}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f8eaf8df3154c790abba9209c6e6bfd6_l3.png)
Lösung:

D =
-
Kürze den Bruchterm:
![Rendered by QuickLaTeX.com \[\frac{(x + 2)(x-3)}{2(x - 3)}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8f3031ea0a026375b0ef253240068835_l3.png)
Lösung:

D =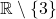
-
Erweitere den Bruchterm:
![Rendered by QuickLaTeX.com \[\frac{5}{x - 1} \text{ mit } (x + 3)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-94a1f62b311a0455fe25735a18af8cf4_l3.png)
Lösung:

D =
-
Erweitere den Bruchterm:
![Rendered by QuickLaTeX.com \[\frac{3}{x + 2} \text{ mit } (x - 2)\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ccca97d0f3024f8b449e4da514c9cd12_l3.png)
Lösung:

D =
-
Addiere die Brüche:
![Rendered by QuickLaTeX.com \[\frac{3}{x-1} + \frac{2}{x+1}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b212345dde841810cebc95d7003bde10_l3.png)
Lösung:

D =
-
Addiere die Brüche:
![Rendered by QuickLaTeX.com \[\frac{5}{2x} + \frac{3}{3x}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-e5d8782298d31bf3d9012f6f246ab10f_l3.png)
Lösung:

D =
-
Subtrahiere die Brüche:
![Rendered by QuickLaTeX.com \[\frac{2x}{x+3} - \frac{1}{(x+3)^2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3a40636bbb5c8bd4492ed7a5853b5bba_l3.png)
Lösung:

D =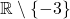
-
Subtrahiere die Brüche:
![Rendered by QuickLaTeX.com \[\frac{5}{x-2} - \frac{3}{(x-2)^2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-46e1a482ea2b45e9c1fbe464b1fef889_l3.png)
Lösung:

D =
-
Multipliziere die Brüche:
![Rendered by QuickLaTeX.com \[\frac{4}{x-1} \cdot \frac{2x}{x+2}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-460c0489aba8434d4e37f29f5feb4a9f_l3.png)
Lösung:

D =
-
Multipliziere die Brüche:
![Rendered by QuickLaTeX.com \[\frac{3}{x+5} \cdot \frac{x-3}{2x}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-4e3d78002890c4bc11ea4cbc180e8fd5_l3.png)
Lösung:

D =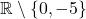
-
Dividiere die Brüche:
![Rendered by QuickLaTeX.com \[\frac{1}{x-3} \div \frac{x+2}{10-x}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-041608464df0f28f3f122e26c3f16ef8_l3.png)
Lösung:

D =
-
Dividiere die Brüche:
![Rendered by QuickLaTeX.com \[\frac{2}{x+4} \div \frac{x-1}{x+3}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a19c1e258ed9dceeb7eb6c6158f5d371_l3.png)
Lösung:

D =
Bruchtherme — häufigste Fragen
(ausklappen)
Bruchtherme — häufigste Fragen
(ausklappen)-
Was ist ein Bruchtherm?Ein Bruchterm ist ein spezieller Bruch, der mindestens eine Variable im Nenner enthält. Er kann aber auch Variablen im Zähler enthalten. Beim Umformen von Bruchtermen gelten dieselben Regeln wie bei Brüchen, Gleichungen und Termen.
-
Wie bilde ich den Kehrwert eines Bruchterms?Den Kehrwert eines Bruchterms kannst du genauso bilden wie den Kehrwert eines Bruchs. Dazu vertauscht du einfach nur den Zähler und Nenner. Das nutzt du z. B. wenn du zwei Brüche dividierst. Dann multiplizerst du nämich einfach den ersten Bruch mit dem Kehrwert des zweiten.
-
Wie komme ich auf den gemeinsamen Nenner?Am einfachsten findest du den gemeinsamen Nenner von zwei Bruchtermen, wenn du ihre jeweiligen Nenner miteinander mulitplizierst. Vergiss nicht, auch die Zähler mit dem Term mal zu nehmen!
Z. B.![Rendered by QuickLaTeX.com \[\frac{1}{x} - \frac{3}{2 - x} = \]](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-d33da9d5e19b94851a98630817209f2a_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{x} \cdot \frac{x - 2}{x - 2} - \frac{3}{x - 2} \cdot \frac{x}{x} =\]](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-0bae9de6e5cd0370dc8e4b4e56a8307d_l3.png)
![Rendered by QuickLaTeX.com \[\frac{x - 2}{x(x - 2)} - \frac{3x}{x(x - 2)}\]](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-d430ba7163b5e00eb3a336c69476e28f_l3.png)
Bruchrechnen
Jetzt hast du alle Informationen rund ums Thema Bruchterme! Du möchtest lieber nochmal die Grundlagen wiederholen? Dann schau hier in unseren Beitrag zum Thema Bruchrechnen an.

