Brüche kürzen

Was bedeutet „Brüche kürzen“?

Wenn du einen Bruch kürzt, teilst du sowohl den Zähler als auch den Nenner durch die gleiche Zahl.

Du hast zum Beispiel den Bruch ​. Zähler und Nenner kannst du beide durch 2 teilen und somit den Bruch kürzen. So wird daraus:

Beide Brüche — und — beschreiben dieselbe Menge. Der Bruch hat nur kleinere Zahlen. Das ist praktisch, wenn du mit dem Bruch rechnen willst. Beim Kürzen geht es also darum, einen Bruch übersichtlicher und handlicher zu machen.

Wie kürzt du einen Bruch?

Damit du einen Bruch kürzen kannst, brauchst du eine Zahl, durch die sowohl der Zähler als auch der Nenner geteilt werden können. Die größte solche Zahl nennst du den größten gemeinsamen Teiler (ggT).

Schauen wir uns das an einem Beispiel an: Du hast den Bruch und möchtest ihn kürzen. Nun gehst du so vor:

1. Größten gemeinsamen Teiler finden
Du suchst eine Zahl, durch die 42 und 56 ohne Rest teilbar sind — und zwar die größte dieser Zahlen (ggT).

So findest du ihn:

• Liste alle Teiler von 42 auf: 1, 2, 3, 6, 7, 14, 21, 42
• Liste alle Teiler von 56 auf: 1, 2, 4, 7, 8, 14, 28, 56

Gemeinsame Teiler: 1, 2, 7, 14
→ Der größte gemeinsame Teiler ist 14

2. Zähler und Nenner durch den ggT teilen
Teile jetzt beide Zahlen durch 14:

42 ÷ 14 = 3
56 ÷ 14 = 4

3. Ergebnis aufschreiben
Der gekürzte Bruch ist

Damit bist du fertig!

Tipp: Du musst nicht direkt mit dem größten gemeinsamen Teiler kürzen — vor allem, wenn der nicht leicht zu finden ist. Starte einfach mit kleineren Teilern und arbeite dich so bis zum gekürzten Ergebnis vor. Zum Beispiel:

Brüche kürzen beim Addieren und Subtrahieren

Wenn du Brüche addieren oder subtrahieren möchtest, brauchst du gleichnamige Brüche — also Brüche mit dem gleichen Nenner. Sind sie jedoch ungleichnamig, musst du die Brüche auf einen gemeinsamen Nenner bringen. Das kannst du durch Kürzen erreichen.

Schauen wir uns das am Beispiel + an:

1. Gemeinsamen Nenner finden
Überlege zuerst, welcher Nenner sich für beide Brüche eignet.

Die 16 ist das doppelte von 8. Beide haben also den gemeinsamen Nenner 8.
→ Also bringen wir beide Brüche auf Achtel und du musst nur einen der Brüche kürzen.

2. Auf den gemeinsamen Nenner kürzen
bleibt wie es ist.
musst du auf Achtel kürzen:

=

Jetzt sind beide Brüche gleichnamig:

+

3. Brüche addieren
+ =

kannst du noch weiter kürzen — nämlich durch 4:
= ​

5 Tipps zum Kürzen von Brüchen

Bevor du mit dem Kürzen loslegst, gibt es ein paar einfache Tipps, die du kennen solltest. Sie helfen dir dabei, Brüche richtig zu vereinfachen.

1. Nie durch 0 teilen
   Beim Kürzen darfst du nicht durch 0 teilen. Das ist in der Mathematik grundsätzlich verboten. Denn durch 0 zu teilen, ergibt kein sinnvolles Ergebnis.
   ➡️ Beispiel:  
    
2. Negative Brüche kürzt du wie normale Brüche
   Wenn ein Bruch negative Zahlen enthält, kannst den Bruch trotzdem ganz normal mit einer positiven Zahl kürzen. Das Minuszeichen setzt du dann vor das Ergebnis.
   ➡️ Beispiel: Statt durch -3 zu teilen, nimmst du einfach +3. Das sieht dann so aus:
    
3. Kürzen nur mit echten Teilern
   Teile nicht durch die Zahl selbst, wenn das keinen Vorteil bringt.
   ➡️ Beispiel: 
   Der Bruch ist dann kein Bruch mehr, sondern nur noch eine Zahl. Kürzen ergibt also nur Sinn, wenn danach ein Bruch übrig bleibt.
    
4. Nutze einfache Teilbarkeitsregeln als Abkürzung
   Du musst nicht immer alle Teiler aufschreiben. Die Teilbarkeitsregeln helfen dir auf einen Blick:
   • Gerade Zahl? → durch 2 teilbar
   • Endet auf 0 oder 5? → durch 5 teilbar
   • Quersumme durch 3 teilbar? → durch 3 teilbar
       
5. Wenn Kürzen nicht geht, hilft Erweitern
   In manchen Fällen lässt sich ein Bruch nicht kürzen — du musst ihn aber trotzdem an einen anderen Bruch anpassen, zum Beispiel beim Addieren. Dann kannst du den Bruch erweitern, um ihn auf denselben Nenner wie den anderen Bruch zu bringen.
   ➡️ Beispiel: + ​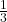
   Hier kannst du keinen Bruch kürzen, damit die Nenner gleich werden — aber du kannst beide Brüche erweitern: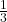 = , = . Jetzt kannst du rechnen: + =

Übungsaufgaben zum Kürzen von Brüchen

Nun kannst du mit unseren Aufgaben selbst ausprobieren, ob du den größten gemeinsamen Teiler findest und die Brüche richtig kürzt.

Aufgabe 1: Kürze den Bruch

Lösung:
ggT = 5
Ergebnis = 2/3

Aufgabe 2: Kürze den Bruch

Lösung:
ggT = 7
Ergebnis = 7/2

Aufgabe 3: Kürze den Bruch

Lösung:
ggT = 5
Ergebnis = 1/5

Aufgabe 4: Kürze den Bruch

Lösung:
ggT =42
Ergebnis = 2/3

Aufgabe 5: Kürze den Bruch

Lösung:
ggT = 36
Ergebnis = 4/5

Aufgabe 6: Kürze den Bruch

Lösung:
ggT = 75
Ergebnis = 3/4

Aufgabe 7: Kürze den Bruch

Lösung:
ggT = 33
Ergebnis = 6/7

Brüche erweitern

Brüche kannst du nicht nur kürzen, sondern auch vergrößern, ohne ihren Wert zu verändern. Wie das funktioniert, zeigen wir dir im Beitrag zum Brüche erweitern.