Video

Quiz

Hier geht's zum Video „Ausmultiplizieren und Ausklammern“

Hier geht's zum Video „Parameterform“

Hier geht's zum Video „Parameterform in Koordinatenform“

Hier geht's zum Video „Normalenvektor“

Hier geht's zum Video „Kreuzprodukt / Vektorprodukt“

Hier geht's zum Video „Schnittgerade zweier Ebenen“

Schnittpunkt Gerade Ebene

Wichtige Inhalte in diesem Video

Schnittpunkt Gerade Ebene einfach erklärt

Schnittpunkt aus Parameterform berechnen

Du möchtest wissen, was ein Schnittpunkt zwischen einer Geraden und einer Ebene ist und wie du ihn berechnen kannst? Dann ist dieser Artikel und unser Video genau das Richtige für dich!

Inhaltsübersicht

Schnittpunkt Gerade Ebene einfach erklärt

im Videozur Stelle im Video springen

Der Schnittpunkt einer Geraden mit einer Ebene ist der Punkt, an dem die Gerade die Ebene schneidet, also durch sie hindurchgeht. Schau dir dazu folgende Gerade g und Ebene E an:

$\textcolor{blue}{g: \vec{x} = \left(\begin{array}{r}\textcolor{red}{1}\\\textcolor{blue}{2}\\\textcolor{green}{3}\\\end{array}\right) + r \left(\begin{array}{r}\textcolor{red}{1}\\\textcolor{blue}{0}\\\textcolor{green}{1}\\\end{array}\right)} \qquad \text{und} \qquad \textcolor{orange}{E: 2 x_1 + 2 x_2 - 3 x_3 = 20}$

Den Schnittpunkt kannst du nun ganz leicht Schritt für Schritt berechnen:

Schritt 1: Schreibe die Geradengleichung g in eine einzige große Klammer:
$\textcolor{blue}{\left(\begin{array}{r}\textcolor{red}{1 + r \cdot 1}\\\textcolor{blue}{2 + r \cdot 0}\\\textcolor{green}{3 + r \cdot 1 }\end{array}\right)}= \left( \begin{array}{r}\textcolor{red}{ x_1}\\\textcolor{blue}{x_2}\\\textcolor{green}{x_3}\\\end{array}\right)$

Schritt 2: Setze die Zeilen von g in E ein:
$\textcolor{orange}{2}\cdot\textcolor{red}{( 1+ r \cdot 1)} \textcolor{orange}{+2}\cdot\textcolor{blue}{( 2+ r \cdot 0)}\textcolor{orange}{ -3}\cdot\textcolor{green}{( 3+r \cdot 1)}\textcolor{orange}{= 20}$

Schritt 3: Multipliziere aus und löse nach Parameter r auf:
$\begin{align*} &2\cdot( 1+ r \cdot 1) + 2\cdot( 2+ r \cdot 0) -3 \cdot(3+r \cdot 1)= 20 \\ \implies &2+ 2r+ 4- 9- 3r = 20 \\\implies &\textcolor{olive}{r = -23}\end{align*}$

Schritt 4: Setze r in g ein:
$\vec{S} = \textcolor{blue}{\left( \begin{array}{r}1\\2\\3\\\end{array}\right) + }\textcolor{olive}{(-23)}\textcolor{blue}{ \left(\begin{array}{r}1\\0\\1\\\end{array}\right)} = \textcolor{red}{\left( \begin{array}{r}-22\\2\\-20\\\end{array}\right)}$

Schritt 5: Lies den Schnittpunkt S ab:
Die Gerade g und die Ebene E schneiden sich im Punkt S (-22 | 2 | -20).

Schnittpunkt aus Parameterform berechnen

im Videozur Stelle im Video springen

Du hast deine Ebenengleichung in Parameterform und nicht wie oben in Koordinatenform vorliegen? Dann schau dir dieses Beispiel an:

$\textcolor{blue}{g: \vec{x} = \left( \begin{array}{r}\textcolor{red}{1}\\\textcolor{blue}{1}\\\textcolor{green}{7}\\\end{array}\right) + r \left(\begin{array}{r}\textcolor{red}{2}\\\textcolor{blue}{3}\\\textcolor{green}{4}\\\end{array}\right)} \qquad \text{und} \qquad E: \vec{x} = \textcolor{gray}{\left( \begin{array}{r}1\\2\\4\\\end{array}\right)} + \textcolor{purple} {\lambda \left(\begin{array}{r}1\\0\\1\\\end{array}\right)} + \textcolor{purple}{\mu \left(\begin{array}{r}0\\1\\-2\\\end{array}\right)}$

Als Erstes wandelst du nun die Ebene von der Parameterform in die Koordinatenform um . Auch hier gehst du Schritt für Schritt vor.

Schritt 1: Berechne das Kreuzprodukt der beiden Spannvektoren. Daraus erhältst du den Normalenvektor n:
$\textcolor{magenta}{\vec{n}}= \textcolor{purple}{ \left(\begin{array}{r}1\\0\\1\\\end{array}\right) \textcolor{black}{\times} \left(\begin{array}{r}0\\1\\-2\\\end{array}\right)} = \textcolor{magenta}{\left(\begin{array}{r}-1\\2\\1\\\end{array}\right)}$

Schritt 2: Jetzt kannst du schon fast deine ganze Koordinatenform hinschreiben. Die Grundlage deiner Koordinatenform bilden x₁, x₂ und x₃. Stelle der Reihe nach die drei Koordinaten vom Normalenvektor n jeweils vor x₁, x₂ und x₃. Diese Formel setzt du nun mit dem Parameter c gleich. Schreibe also auf die rechte Seite des Gleichzeichens ein c:
$E: \textcolor{magenta}{-1}x_1 + \textcolor{magenta}{2}x_2+\textcolor{magenta}{1} x_3 = c$

Schritt 3: Setze jetzt den Stützvektor für x₁, x₂ und x₃ in die Koordinatenform ein und löse nach c auf:
$E: \textcolor{magenta}{-1} \cdot \textcolor{gray}{1} \textcolor{magenta}{+ 2} \cdot\textcolor{gray}{ 2} \textcolor{magenta}{+ 1} \cdot \textcolor{gray}{4} = c \\ \implies 7 = c$

Schritt 4: Setze den Parameter c jetzt in die Koordinatenform ein:
$E: \textcolor{magenta}{-1}x_1 + \textcolor{magenta}{2}x_2+ \textcolor{magenta}{1}x_3 = 7$

Prima! Jetzt kannst du loslegen, den Schnittpunkt von der Geraden g und der Ebene E zu berechnen!

$\textcolor{blue}{g: \vec{x} = \left( \begin{array}{r}\textcolor{red}{1}\\\textcolor{blue}{1}\\\textcolor{green}{7}\\\end{array}\right) + r \left(\begin{array}{r}\textcolor{red}{2}\\\textcolor{blue}{3}\\\textcolor{green}{4}\\\end{array}\right)}$

$\textcolor{orange}{E: -x_1 + 2x_2+ x_3 = 7}$

Rechne dafür wieder die 5 Schritte wie oben im Beispiel:

Schritt 1: Schreibe die Geradengleichung g in eine einzige große Klammer:
$\textcolor{blue}{\left(\begin{array}{r}\textcolor{red}{1 + r \cdot 2}\\\textcolor{blue}{1 + r \cdot 3}\\\textcolor{green}{7 + r \cdot 4}\end{array}\right)}= \left( \begin{array}{r} \textcolor{red}{x_1}\\\textcolor{blue}{x_2}\\\textcolor{green}{x_3}\\\end{array}\right)$

Schritt 2: Setze die Zeilen von g in E ein:
$\textcolor{orange}{-1}\cdot \textcolor{red}{( 1+ r \cdot 2)}\textcolor{orange}{ + 2}\cdot \textcolor{blue}{( 1+ r \cdot 3)}\textcolor{orange}{ +1}\cdot \textcolor{green}{( 7+r \cdot 4)}\textcolor{orange}{= 7}$

Schritt 3: Multipliziere aus und löse nach Parameter r auf:
$\begin{align*} &-1\cdot ( 1+ r \cdot 2) + 2\cdot ( 1+ r \cdot 3) +1\cdot ( 7+r \cdot 4)= 7 \\\implies &-1 -2r+ 2 + 6r+ 7 +4r= 7\\\implies &\textcolor{olive}{r= -0,125}\end{align*}$

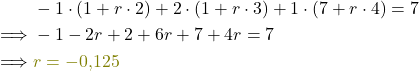
Schritt 4: Setze r in g ein:
$\vec{S} =\textcolor{blue}{ \left( \begin{array}{r}1\\1\\7\\\end{array}\right) +}\textcolor{olive}{ (-0,125)}\textcolor{blue}{ \left(\begin{array}{r}2\\3\\4\\\end{array}\right) = }\textcolor{red}{\left( \begin{array}{r}0,75\\0,625\\6,5\\\end{array}\right)}$

Schritt 5: Lies den Schnittpunkt S ab:
Der Schnittpunkt von Gerade und Ebene liegt bei S (0,75 | 0,625 | 6,5).

Übungsaufgaben: Schnittpunkt Gerade Ebene

Super! Wende dein Wissen gleich bei einer Schnittpunktberechnung in Koordinaten- und in Parameterform an. Los geht´s!

Aufgabe 1: Berechne den Schnittpunkt der Ebene E mit der Geraden g.

$\textcolor{blue}{g: \vec{x} = \left(\begin{array}{r}\textcolor{red}{0}\\\textcolor{blue}{1}\\\textcolor{green}{4}\\\end{array}\right) + r \left(\begin{array}{r}\textcolor{red}{2}\\\textcolor{blue}{1}\\\textcolor{green}{1}\\\end{array}\right)}$

$\textcolor{orange}{E: 1x_1 +2x_2 - 1x_3 = 40}$

Lösung:

Schritt 1: Schreibe die Geradengleichung g in eine einzige große Klammer:
$\textcolor{blue}{\left(\begin{array}{r}\textcolor{red}{0 + r \cdot 2}\\\textcolor{blue}{1 + r \cdot 1}\\\textcolor{green}{4 + r \cdot 1} \end{array}\right)}= \left( \begin{array}{r}\textcolor{red}{x_1}\\\textcolor{blue}{x_2}\\\textcolor{green}{x_3}\\\end{array}\right)$

Schritt 2: Setze die Zeilen von g in E ein:
$\textcolor{orange}{1}\cdot \textcolor{red}{( 0+ r \cdot 2)}\textcolor{orange}{ + 2}\cdot \textcolor{blue}{( 1+ r \cdot 1)}\textcolor{orange}{ -1}\cdot \textcolor{green}{( 4+r \cdot 1)}\textcolor{orange}{= 40}$

Schritt 3: Multipliziere aus und löse nach r auf:
$\begin{align*}&1\cdot( 0+ r \cdot 2) + 2 \cdot ( 1+\cdot r \cdot 1) -1\cdot ( 4+r \cdot 1)= 40\\ \implies &2r+ 2+ 2r- 4- r = 40\\ \implies &\textcolor{olive}{r = 14}\end{align*}$

Schritt 4: Setze r in g ein:
$\vec{S} =\textcolor{blue}{ \left( \begin{array}{r}0\\1\\4\\\end{array}\right) }\textcolor{olive}{ +14} \cdot \textcolor{blue}{ \left(\begin{array}{r}2\\1\\1\\\end{array}\right)} = \textcolor{red}{\left( \begin{array}{r}28\\15\\18\\\end{array}\right)}$

Schritt 5: Lies den Schnittpunkt S ab:
Der Schnittpunkt liegt bei S (28 | 15 | 18).

Aufgabe 2: Berechne den Schnittpunkt der Ebene E mit der Geraden g.

$\textcolor{blue}{g: \vec{x} = \left( \begin{array}{r}\textcolor{red}{2}\\\textcolor{blue}{1}\\\textcolor{green}{2}\\\end{array}\right) + r \left(\begin{array}{r}\textcolor{red}{-2}\\\textcolor{blue}{-1}\\\textcolor{green}{-1}\\\end{array}\right)}$

$E: \vec{x} = \textcolor{gray}{\left( \begin{array}{r}1\\1\\4\\\end{array}\right)} +\textcolor{purple}{ \lambda \left(\begin{array}{r}1\\0\\1\\\end{array}\right) + \mu \left(\begin{array}{r}0\\1\\2\\\end{array}\right)}$

Lösung:

Als erstes musst du die Ebene von der Parameterform in Koordinatenform umrechnen:

Schritt 1: Berechne den Normalenvektor als Kreuzprodukt der beiden Spannvektoren:
$\textcolor{magenta}{\vec{n}}= \textcolor{purple}{\left(\begin{array}{r}1\\0\\1\\\end{array}\right) \textcolor{black}{\times} \left(\begin{array}{r}0\\1\\2\\\end{array}\right)} =\textcolor{magenta}{ \left(\begin{array}{r}-1\\-2\\1\\\end{array}\right)}$

Schritt 2: Schreibe die Koordinaten vom Normalenvektor n jeweils vor x₁, x₂ und x₃:
$E: \textcolor{magenta}{-1}x_1 \textcolor{magenta}{- 2}x_2+ \textcolor{magenta}{1}x_3 = c$

Schritt 3: Bestimme den Parameter c mit dem Stützvektor:
$\begin{align*}&E: \textcolor{magenta}{-1} \cdot \textcolor{gray}{1} \textcolor{magenta}{- 2} \cdot \textcolor{gray}{1}\textcolor{magenta}{+ 1} \cdot \textcolor{gray}{4} = c \\ &\implies 1= c \end{align*}$

Schritt 4: Setze den Parameter c nun noch in die Koordinatenform ein:
$E: \textcolor{magenta}{-1} x_1 \textcolor{magenta}{- 2} x_2 + \textcolor{magenta}{1} x_3 = 1$

Berechne nun den Schnittpunkt S von der Gerade g und der Ebene E. Nutze dafür wieder die 5 Schritte von oben:

$\textcolor{blue}{g: \vec{x} = \left( \begin{array}{r}\textcolor{red}{2}\\\textcolor{blue}{1}\\\textcolor{green}{2}\\\end{array}\right) + r \left(\begin{array}{r}\textcolor{red}{-2}\\\textcolor{blue}{-1}\\\textcolor{green}{-1}\\\end{array}\right)}$

$\textcolor{orange}{E: -x_1 - 2x_2+ x_3 = 1}$

Schritt 1: Schreibe die Geradengleichung g in eine einzige große Klammer:
$\textcolor{blue}{\left(\begin{array}{r}\textcolor{red}{2 + r \cdot (-2)}\\\textcolor{blue}{1 + r \cdot (-1)}\\\textcolor{green}{2 + r \cdot (-1)} \end{array}\right)}= \left( \begin{array}{r}\textcolor{red}{ x_1}\\\textcolor{blue}{x_2}\\\textcolor{green}{x_3}\\\end{array}\right)$

Schritt 2: Setze die Zeilen von g in E ein:
$\textcolor{orange}{-1}\cdot \textcolor{red}{( 2+ r \cdot (-2))}\textcolor{orange}{ - 2}\cdot \textcolor{blue}{( 1+ r \cdot (-1))}\textcolor{orange}{ +1}\cdot \textcolor{green}{( 2+ r \cdot (-1))}\textcolor{orange}{= 1}$

Schritt 3: Multipliziere aus und löse nach r auf:
$\begin{align*} &-1\cdot ( 2+ r \cdot -2) - 2\cdot (1+ r \cdot -1) +1\cdot ( 2+ r \cdot -1)= 1 \\ \implies &-2+ 2r- 2+ 2r+ 2 -r = 1\\ \implies &\textcolor{olive}{r= 1}\end{align*}$

Schritt 4: Setze r in g ein:
$\vec{S} = \textcolor{blue}{\left( \begin{array}{r}2\\1\\2\\\end{array}\right)}\textcolor{olive}{ +1}\textcolor{blue}{ \left(\begin{array}{r}-2\\-1\\-1\\\end{array}\right) =}\textcolor{red}{ \left( \begin{array}{r}0\\0\\1\\\end{array}\right)}$

Schritt 5: Lies den Schnittpunkt S ab:
Der Schnittpunkt liegt bei S (0 | 0 | 1).

Lagebeziehungen Gerade Ebene

Gerade und Ebene schneiden sich aber nicht immer. Es gibt drei verschiedene Möglichkeiten, wie Geraden und Ebenen zueinander liegen können:

1. Die Gerade schneidet die Ebene. Es gibt genau eine Lösung für den Schnittpunkt:

Schnittpunkt Gerade Ebene, Schnittpunkt Ebene Gerade, Durchstoßpunkt Gerade Ebene, Koordinatensystem, Schnittpunkt, Gerade, Ebene, dreidimensionaler Raum — Die Gerade schneidet die Ebene im Schnittpunkt S.

2. Die Gerade verläuft parallel zur Ebene. Gerade und Ebene schneiden sich nicht. Es gibt also keine Lösung für einen Schnittpunkt.

Gerade Ebene parallel, kein Schnittpunkt Gerade Ebene, kein Schnittpunkt Ebene Gerade, Durchstoßpunkt Gerade Ebene, Koordinatensystem, kein Schnittpunkt, Gerade, Ebene, dreidimensionaler Raum — Die Gerade und die Ebene sind parallel und haben keinen Schnittpunkt.

3. Die Gerade liegt in der Ebene. Gerade und Ebene schneiden sich die ganze Zeit. Es gibt also unendlich viele Lösungen für einen Schnittpunkt.

Gerade liegt in Ebene, Gerade Ebene parallel, Schnittpunkt Gerade Ebene, Schnittpunkt Ebene Gerade, permanenter Durchstoßpunkt Gerade Ebene, Koordinatensystem, permanenter Schnittpunkt, Gerade, Ebene, dreidimensionaler Raum — Die Gerade liegt in der Ebene, sie schneiden sich die ganze Zeit.

Schnittgerade zweier Ebenen

Jetzt hast du gelernt, was ein Schnittpunkt zwischen Gerade und Ebene ist und wie man diesen berechnet. Was machst du aber, wenn du die Schnittgerade zweier Ebenen berechnen sollst? Das erfährst du hier !

Zum Video: Schnittgerade zweier Ebenen

zur Videoseite: Schnittpunkt Gerade Ebene

Beliebte Inhalte aus dem Bereich Geometrie

Koordinatenform

Hessesche Normalform

Ebenengleichung

Schnittgerade zweier Ebenen

Schnittpunkt Gerade Ebene

Koordinatenform in Parameterform

Parameterform in Koordinatenform

Thema präsentiert von unserem Werbepartner

Zur Webseite

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Bitte .