Zusammengesetzte Körper
Um zusammengesetzte Körper berechnen zu können, musst du dich gut mit den Grundkörpern auskennen. Wie genau das geht, erfährst du hier und im Video.
Inhaltsübersicht
Zusammengesetzte Körper — einfach erklärt
Ein zusammengesetzter Körper ist ein Körper, der aus mindestens zwei zusammengesteckten einfachen Körpern besteht. Dazu zählen Würfel, Quader, Zylinder, Pyramiden und Kugeln.
Um das Volumen oder die Oberfläche von einem zusammengesetzten Körper zu berechnen, zerlegst du ihn in seine einzelnen Formen. Dann berechnest du die Größen für die einzelnen Körper, bevor du sie addierst. Es ist also wichtig, dass du die Formeln der einfachen Körper kennst.
| Körper | Volumen | Oberfläche |
| Würfel |  |
 |
| Quader |  |
 |
| Zylinder |  |
 |
| Pyramide |  |
 |
| Kugel |  |
 |
Zusammengesetzte Körper — Volumen berechnen
Um das Volumen eines zusammengesetzten Körpers zu berechnen, musst du die einzelnen Bestandteile erkennen und ihre Volumenformeln wissen. Du berechnest dann die einzelnen Volumen und addierst sie schließlich. Schauen wir uns das anhand folgendem Beispiel an:
Angenommen, du hast ein Spielhaus. Die Wohnfläche des Hauses ist dabei ein Würfel und misst für jede Seite a 4 cm. Das Dach besteht aus einer Pyramide mit einer Höhe (h) von 6 cm, einer quadratischen Grundfläche (G) mit 4 cm für alle Seitenlängen und einer Seitenflächenhöhe (hs) von 12 cm.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Spielhaus Volumen berechnen
Um das Volumen zusammengesetzter Körper zu berechnen, hast du zwei Möglichkeiten. Gehen wir beide für das Volumen des Spielhauses durch.
Volumen Spielhaus — erster Rechenweg
Beim ersten Weg gehst du wie folgt vor:
-
Zerlege den zusammengesetzten Körper in seine einfachen Bestandteile.
Das Spielhaus besteht aus zwei Körpern: einem Würfel und einer Pyramide.
Bestandteile des Spielhauses -
Verwende die entsprechenden Formeln, um das Volumen jedes Einzelteils zu berechnen.
Dafür benötigst du folgende Fomeln:


![Rendered by QuickLaTeX.com V_{\text{Würfel}}= 64 [cm^3]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3aca55f172e78416f9d56bb38b4e9dce_l3.png)




![Rendered by QuickLaTeX.com V_{\text{Pyramide}}= 32 [cm^3]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-657a946ebe114107cefe2c6cb81fde1e_l3.png)
-
Addiere die Volumina der Einzelteile, um das Gesamtvolumen zu erhalten.


![Rendered by QuickLaTeX.com V_{\text{gesamt}}=96 [cm^3]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-4998f69d3dc3fbb364f2241fe7c5485a_l3.png)
Das Spielhaus hat also ein Gesamtvolumen von 96 cm³.
Volumen Spielhaus — zweiter Rechenweg
Beim zweiten Weg berechnest du die Volumen der Teilkörper gleich gemeinsam. Du musst sie am Schluss also nicht nochmal addieren.
-
Zerlege den zusammengesetzten Körper in seine einfachen Bestandteile.
Das Spielhaus besteht aus zwei Körpern: einem Würfel und einer Pyramide.
-
Addiere die beiden Volumenformeln und berechne das Gesamtvolumen.






![Rendered by QuickLaTeX.com V_{\text{gesamt}}=96 [cm^3]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-4998f69d3dc3fbb364f2241fe7c5485a_l3.png)
Auch über den zweiten Weg erhältst du für das Spielhaus ein Gesamtvolumen von 96 cm³. Es spielt also keine Rolle, welchen Weg du nimmst.
Wichtig: Der zweite Weg ist etwas genauer als der erste, da keine Rundungsfehler auftreten.
Zusammengesetzte Körper — Oberfläche berechnen
Auch um die Oberfläche von zusammengesetzten Körpern zu berechnen, siehst du dir zuerst an, aus welchen Einzelteilen er besteht.
Wichtig: Von der Gesamtoberfläche musst du die gemeinsame Fläche der beiden Körper abziehen! Das ist die Fläche, an der sich die Körper berühren. Sie zählt also nicht zur Oberfläche, sondern zum Innenraum.
Spielhaus Oberfläche berechnen
Wir betrachten wieder unser Beispiel von oben und folgen dem ersten Rechenweg. Du berechnest die Oberflächen der Einzelteile also nacheinander.
-
Zerlege den zusammengesetzten Körper in seine einfachen Bestandteile.
Das Spielhaus besteht aus zwei Körpern: einem Würfel und einer Pyramide.
-
Verwende die entsprechenden Formeln, um die Oberfläche jedes Einzelteils zu berechnen.


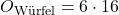
![Rendered by QuickLaTeX.com O_{\text{Würfel}}= 96 [cm^2]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d445206a65d91333365b6d010e635e65_l3.png)
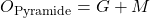
Um die Oberfläche der Pyramide zu berechnen, brauchst du die Größen G (Grundfläche) und M (Mantelfläche). Da du jedoch nur die Seitenlänge (a), die Höhe (h) und die Seitenflächenhöhe (hs) gegeben hast, kannst du die Formel wie folgt umschreiben:

 .
.
n ist dabei die Anzahl der Ecken der Pyramide. Hier also 4. Die beiden Formeln setzt du nun anstelle von G und M in die Oberflächenformel der Pyramide ein. Dadurch erhältst du folgende Gleichung, mit der du nun die Oberfläche berechnen kannst:





![Rendered by QuickLaTeX.com O_{\text{Pyramide}}=112[cm^2]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-40982be3b5f967d87d0c2935e549578b_l3.png)
-
Berechne die gemeinsame Fläche.
Um herauszufinden, wie groß die gemeinsame Fläche ist, schauen wir uns nochmal die Abbildung an.
Gemeinsame Fläche
Die Pyramide sitzt auf dem Würfel. Dabei berührt die obere Seite des Würfels die Grundfläche der Pyramide. Die gemeinsame Fläche beträgt also 2 · a².




Sie ziehst du nun von der Gesamtoberfläche ab.
-
Addiere die beiden Oberflächen und ziehe die gemeinsamen Flächen ab.



![Rendered by QuickLaTeX.com O_{\text{gesamt}}=176 [cm^2]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-16305b6d1c0403e141751f34b2302225_l3.png)
Die Gesamtoberfläche des Spielhauses beträgt also 176 cm².
Du kannst die Oberfläche auch mithilfe des zweiten Wegs berechnen. Dafür sieht die Formel dann so aus:


Zusammengesetzte Körper — häufigste Fragen
(ausklappen)
Zusammengesetzte Körper — häufigste Fragen
(ausklappen)-
Was sind zusammengesetzte Körper in Mathe?Zusammengesetzte Körper in Mathe sind Körper, die aus mindestens zwei einfachen Grundkörpern zusammengesetzt sind, zum Beispiel aus Würfel, Quader, Zylinder, Pyramide oder Kugel. Du kannst sie dir wie „zusammengesteckte“ Bauteile vorstellen. Für Rechnungen zerlegst du sie gedanklich wieder in diese Teile.
-
Wie erkenne ich bei einem zusammengesetzten Körper die einzelnen Grundkörper?Die einzelnen Grundkörper erkennst du, indem du nach typischen Formen suchst und den Körper gedanklich „zerschneidest“. Achte auf runde Teile (Zylinder oder Kugel) und eckige Teile (Würfel oder Quader). Beispiel: Ein „Haus“ ist oft ein Quader als Wandteil und eine Pyramide als Dach.
-
Wie berechne ich das Volumen von einem zusammengesetzten Körper?Das Volumen eines zusammengesetzten Körpers berechnest du, indem du die Volumina der Teilkörper ausrechnest und anschließend addierst. Beispiel: Würfel mit
 hat
hat  , eine Pyramide mit
, eine Pyramide mit  und
und  hat
hat  , also
, also  .
.
-
Wie berechne ich die Oberfläche von einem zusammengesetzten Körper?Die Oberfläche eines zusammengesetzten Körpers berechnest du, indem du die Oberflächen der Teilkörper addierst und dann die gemeinsame Kontaktfläche abziehst, weil sie innen liegt. Beispiel: Zwei Würfel mit
 ergeben
ergeben  , gemeinsame Fläche
, gemeinsame Fläche  , also
, also  .
.
-
Welche Formeln brauche ich am häufigsten für Würfel Quader Zylinder Pyramide und Kugel?Am häufigsten brauchst du diese Formeln: Würfel
 ,
,  ; Quader
; Quader  ,
,  ; Zylinder
; Zylinder  ,
,  ; Pyramide
; Pyramide  ; Kugel
; Kugel  ,
,  .
.
Geometrische Körper
Um einen zusammengesetzten Körper berechnen zu können, ist es hilfreich, wenn du dich gut mit geometrischen Körpern auskennst. Alles Wichtige über sie erfährst du hier!




