Woran erkenne ich, dass eine Gleichung biquadratisch ist?

Du erkennst eine biquadratische Gleichung daran, dass nur x⁴, x² und eine Konstante vorkommen. Dann hat sie die Form und enthält kein x³ oder x. Ein Beispiel ist .

Wie ersetze ich bei der Substitution x² durch z, ohne etwas zu verwechseln?

Du ersetzt bei der Substitution jedes durch z und jedes durch . Das klappt, weil gilt. So wird aus die Gleichung .

Wie löse ich die quadratische Gleichung in z nach der Substitution?

Nach der Substitution löst du die Gleichung in z wie jede normale quadratische Gleichung. Dafür kannst du die pq-Formel verwenden und erhältst z-Werte. Beim Beispiel ergeben sich so und .

Wie mache ich die Resubstitution von z zurück zu x richtig?

Bei der Resubstitution ersetzt du z wieder durch und ziehst dann die Wurzel. Aus jeder Lösung wird also und damit oder . Aus folgen und .

Warum kann bei einer biquadratischen Gleichung am Ende rauskommen, dass es keine reellen Lösungen gibt?

Eine biquadratische Gleichung kann keine reellen Lösungen haben, wenn beim Lösen in z unter der Wurzel eine negative Zahl steht. Dann ist der Wurzelausdruck im Reellen nicht berechenbar. Zum Beispiel führt auf , deshalb gibt es keine Lösung.

Video

Quiz

Hier geht's zum Video „Mitternachtsformel“

Hier geht's zum Video „Potenzgleichungen“

Biquadratische Gleichungen

Wichtige Inhalte in diesem Video

Biquadratische Gleichungen einfach erklärt

(00:13)

Biquadratische Gleichungen lösen

(00:40)

Beispiel 2

(02:44)

Willst du wissen, wie du biquadratische Gleichungen lösen und berechnen kannst? Das erfährst du hier und im Video !

Inhaltsübersicht

Biquadratische Gleichungen einfach erklärt

im Videozur Stelle im Video springen

(00:13)

Die quadratischen Gleichungen der Form ax² + bx + c =0 kennst du bereits. Es gibt aber darüber hinaus noch Gleichungen der Form ax⁴+ bx² + c = 0. Die nennst du auch biquadratische Gleichungen. Sie können beispielsweise so aussehen:

3x⁴+ 2x² + 5 = 0
2x⁴+ x² = 0
x⁴+ 6x² + 1 = 0

Um die Gleichung zu lösen, musst du die sogenannte Substitution anwenden. Dabei ersetzt du in der biquadratischen Gleichungen jedes x²durch ein z. Das kannst du dir an folgenden Beispielen genauer anschauen.

Biquadratische Gleichungen lösen

im Videozur Stelle im Video springen

(00:40)

Zum Lösen von biquadratischen Gleichungen kannst du immer dieselbe Vorgehensweise befolgen. Sieh dir dazu das Beispiel x⁴ – 4x² + 3 = 0 an.

1. Die Substitution funktioniert jetzt so: Ersetze jedes x² durch ein z:
  
  x⁴– 4x² + 3 = 0
  z² – 4z + 3 = 0
  
  Merke! Weil x⁴ = (x²)² ist, kannst du z² schreiben.
2. Die entstandene Gleichung kannst du jetzt wie eine normale quadratische Gleichung lösen. Dafür nutzt du die pq-Formel :
  
  $z_{1/2} = -\frac{-4}{2}\pm \sqrt{(\frac{-4^2}{2)}-3}$
  $z_{1/2} = 2\pm \sqrt{1}$
  $z_{1} = 2 +\sqrt{1}$ = 3
  $z_{2} = 2 - \sqrt{1}$ = 1

Die Lösungen für z sind jetzt also 1 und 3. Du brauchst aber die Lösungen für x. Deshalb musst du die Substitution wieder rückgängig machen. Das nennst du Resubstitution z = x²:

$\begin{array}{rcl}z& =&3\\ x^2&=&3\\ &&\\ x_1=\sqrt{3}&& x_2=-\sqrt{3}\end{array}\quad\quad\quad\quad\quad\begin{array}{rcl}z&=&1\\ x^2&=&1\\ &&\\ x_3=1&& x_4=-1\end{array}$

Super! Du hast die biquadratische Gleichung gelöst.

Übrigens: Du kannst eine biquadratische Gleichung auch mit der Mitternachtsformel lösen. Anstelle der pq-Formel benutzt du im zweiten Schritt einfach die Mitternachtsformel. Mehr dazu erfährst du hier !

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Beispiel 2

im Videozur Stelle im Video springen

(02:44)

Löse noch ein zweites Beispiel: x⁴ + 2x² + 3 = 0

Substitution:
x⁴ + 2x² + 3 = 0
z² + 2z + 3 = 0
PQ-Formel:
$z_{1/2} = -\frac{2}{2}\pm \sqrt{(\frac{2^2}{2)}-3}$
$z_{1/2} = 1\pm \sqrt{-1}$ ❌

Die biquadratische Gleichung hat die diesem Beispiel keine Lösung! Denn aus negativen Zahlen lässt sich keine Wurzel ziehen.

Biquadratische Gleichungen — häufigste Fragen

(ausklappen)

Woran erkenne ich, dass eine Gleichung biquadratisch ist?

Du erkennst eine biquadratische Gleichung daran, dass nur x⁴, x² und eine Konstante vorkommen. Dann hat sie die Form und enthält kein x³ oder x. Ein Beispiel ist .
Wie ersetze ich bei der Substitution x² durch z, ohne etwas zu verwechseln?

Du ersetzt bei der Substitution jedes durch z und jedes durch . Das klappt, weil gilt. So wird aus die Gleichung .
Wie löse ich die quadratische Gleichung in z nach der Substitution?

Nach der Substitution löst du die Gleichung in z wie jede normale quadratische Gleichung. Dafür kannst du die pq-Formel verwenden und erhältst z-Werte. Beim Beispiel ergeben sich so und .
Wie mache ich die Resubstitution von z zurück zu x richtig?

Bei der Resubstitution ersetzt du z wieder durch und ziehst dann die Wurzel. Aus jeder Lösung wird also und damit $x = \sqrt{a}$ oder $x = -\sqrt{a}$ . Aus folgen $x=\sqrt{3}$ und $x=-\sqrt{3}$ .
Warum kann bei einer biquadratischen Gleichung am Ende rauskommen, dass es keine reellen Lösungen gibt?

Eine biquadratische Gleichung kann keine reellen Lösungen haben, wenn beim Lösen in z unter der Wurzel eine negative Zahl steht. Dann ist der Wurzelausdruck im Reellen nicht berechenbar. Zum Beispiel führt auf $\sqrt{-1}$ , deshalb gibt es keine Lösung.

Zusammenfassung

Biquadratische Gleichungen – Das Wichtigste

Du kannst eine biquadratische Gleichung immer mit demselben Verfahren lösen.
- 1. Substitution ( z = x² )
- 2. PQ-Formel oder Mitternachtsformel
- 3. Resubstitution ( z = x² )
Die biquadratische Gleichung kann auch keine Lösung haben. Nämlich, wenn unter der Wurzel eine negative Zahl steht.

Klasse! Du kannst jetzt biquadratische Gleichungen lösen. Willst du auch noch mehr zu Potenzgleichungen erfahren? Dann schau in unser Video dazu rein!
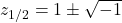