Injektiv Surjektiv Bijektiv Übungsaufgabe I
Betrachten wir nun eine Übungsaufgabe, um dir das Thema näherzubringen:
Entscheide, ob die folgende Abbildung injektiv, surjektiv, oder bijektiv ist. Begründe deine Antwort.

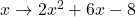
Wie du siehst bildet die betrachtete Funktion die reellen Zahlen wieder auf die reellen Zahlen ab. Das heißt, es lässt sich ein Funktionsgraph zu der Funktion zeichnen. Bei der Lösung der Aufgabe kann es dir helfen, dir zu überlegen wie in etwa dieser Funktionsgraph aussieht.
Ob diese Abbildung injektiv, surjektiv, oder bijektiv ist und wie genau du das mathematisch Bestimmen kannst, siehst du in unserem Video !
Injektiv Surjektiv Bijektiv Übungsaufgabe I — häufigste Fragen
(ausklappen)
Injektiv Surjektiv Bijektiv Übungsaufgabe I — häufigste Fragen
(ausklappen)-
Wie prüfe ich bei einer quadratischen Funktion ohne Graph, ob sie injektiv ist?Eine quadratische Funktion ist auf ℝ nicht injektiv, weil sie nicht streng monoton ist. Du prüfst das ohne Graph über die Symmetrie bzw. den Scheitel: Für
 gilt
gilt  mit
mit  . Damit haben zwei verschiedene x denselben Funktionswert.
. Damit haben zwei verschiedene x denselben Funktionswert.
-
Wie finde ich bei 2x² + 6x – 8 den kleinsten Funktionswert, um zu entscheiden, ob die Funktion surjektiv auf ℝ ist?Der kleinste Funktionswert ist -12, daher ist die Funktion nicht surjektiv auf ℝ. Du bestimmst ihn über den Scheitelpunkt:
 . Einsetzen liefert
. Einsetzen liefert  .
.
-
Was ändert sich an Injektivität und Surjektivität, wenn ich den Definitionsbereich von ℝ auf ein Intervall einschränke?Durch Einschränken auf ein Intervall kann eine quadratische Funktion injektiv werden, surjektiv auf ℝ aber meist nicht. Nimm ein Intervall, auf dem die Funktion streng monoton ist, zum Beispiel
 oder
oder ![Rendered by QuickLaTeX.com (-\infty,-\frac{3}{2}]](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-9d95ecf687f5655581c11bb5b0110b14_l3.png) . Surjektiv auf ℝ wird sie nur, wenn ihr Wertebereich dann ganz ℝ ist, was bei Parabeln nicht klappt.
. Surjektiv auf ℝ wird sie nur, wenn ihr Wertebereich dann ganz ℝ ist, was bei Parabeln nicht klappt.
-
Welche typischen Fehler mache ich bei injektiv, surjektiv und bijektiv, wenn ich nur auf den Graphen schaue?Häufige Fehler sind, die waagerechte Gerade (Injektivität) und die senkrechte Gerade (Funktionstest) zu verwechseln. Außerdem wird der Zielbereich ℝ ignoriert: Eine Parabel wirkt „voll“, trifft aber nicht alle y-Werte, also nicht surjektiv auf ℝ. Auch Randpunkte bei eingeschränkten Intervallen werden leicht übersehen.