DFT – Diskrete Fourier-Transformation
Im folgenden Artikel wird die DFT (Diskrete Fourier Transformation) erklärt und deren Verortung in der Fourier-Analysis dargelegt. Des Weiteren werden wichtige Eigenschaften der DFT gezeigt und außerdem die IDFT (Inverse DFT) erläutert.
Falls dir das zu ausführlich ausfällt, haben wir das Wichtigste zum Thema Diskrete Fourier Transformation für dich in einem anschaulichen Video zusammengefasst.
Inhaltsübersicht
DFT, Fourier Transformation und Fourier Reihen
Die DFT (Diskrete Fourier Transformation) ist eine für die Praxis relevante Transformation aus dem Bereich der Fourier-Analysis.
Die DFT ist mit der kontinuierlichen Fourier-Transformation verwandt und lässt sich aus Überlegungen zu Fourier-Reihen ableiten.
Fourier-Transformation
Mithilfe der Fourier Transformation
lassen sich nichtperiodische Funktionen  durch eine Linearkombination aus Sinus- und Cosinus-Funktionen verschiedener Frequenzen
durch eine Linearkombination aus Sinus- und Cosinus-Funktionen verschiedener Frequenzen 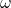 darstellen. Hierfür ordnet die Fourier-Transformierte
darstellen. Hierfür ordnet die Fourier-Transformierte  jeder Frequenz
jeder Frequenz  diejenige Amplitude zu, mit der die Schwingung dieser Frequenz in der Linearkombination auftritt:
diejenige Amplitude zu, mit der die Schwingung dieser Frequenz in der Linearkombination auftritt:
![Rendered by QuickLaTeX.com \hat{f}\left(\omega\right)=\mathcal{F}\left[f\right]\left(\omega\right)\equiv\int_{-\infty}^{\ \ \infty}{\ f\left(t\right)}{\cdot e}^{-i\cdot\omega\cdot t}dt](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-517dd7f1bcc17be5f6e8857e7b2b5a3f_l3.png)
Die nichtperiodischen Funktionen können dann durch das Fourier-Integral – die sogenannte inverse Fourier-Transformierte – genähert werden:
![Rendered by QuickLaTeX.com {f(t)=\mathcal{F}}^{-1}\left[\hat{f}\right]\left(t\right)=\frac{1}{2\pi}\int_{-\infty}^{\ \ \infty}{\hat{f}\left(\omega\right)}{\cdot e}^{i\cdot\omega\cdot t}d\omega](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1c45a5f11fed56d1d01c00227896e9f8_l3.png)
Hierbei fasst die Exponentialfunktion die Sinus- und Cosinus-Schwingungen zusammen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Fourier-Reihen
Für periodische Funktionen f mit der Periode T sind die in der Linearkombination beteiligten Frequenzen diskret. Sie sind ein n-faches der Grundfrequenz 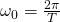 und werden mit
und werden mit  bezeichnet. Aus dem Integral wird damit die Fourier-Reihe
,
bezeichnet. Aus dem Integral wird damit die Fourier-Reihe
,
=\sum_{n=-\infty}^{\infty}c_n\cdot e^{i\cdot\omega_n\cdot t}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d2c79bb850a2825ae2e1433e8948637d_l3.png)
wobei die Amplituden  das Analogon zur Fourier-Transformierten darstellen. Sie lassen sich wie folgt berechnen:
das Analogon zur Fourier-Transformierten darstellen. Sie lassen sich wie folgt berechnen:
 ,
,

Durch die Bestimmung dieser Amplituden bzw. der Fourier-Transformierten werden die betrachteten Funktionen in ihr sogenanntes Frequenzspektrum zerlegt.
Definition: Diskrete Fourier Transformierte
Mithilfe der Fourier-Transformation und der Fourier-Reihe lassen sich also die Frequenzspektren von nichtperiodischen und periodischen Funktionen ermitteln. In der Praxis liegen die zu untersuchenden Signalen allerdings nicht als Funktion vor, sondern als Menge diskreter Werte. Die Diskrete Fourier Transformation befasst sich mit der Spektralanalyse solcher diskreten endlichen Signale, welche zur Untersuchung periodisch fortgesetzt werden.
Untersucht werden sollen die  komplexen Werte
komplexen Werte  , die die Signalwerte darstellen und in einem Vektor
, die die Signalwerte darstellen und in einem Vektor  zusammengefasst werden können.
zusammengefasst werden können.
Die Diskrete Fourier Transformierte  des Vektors
des Vektors  besitzt die Koeffizienten
besitzt die Koeffizienten

Zur Effizienten Berechnung der Diskreten Fourier Transformation gibt die FFT (Fast Fourier Transformation) einen Algorithmus an.
Verwandtschaft zwischen diskreter Fourier-Transformation und Fourier-Reihen
Die DFT ist eng verwandt mit der Theorie der Fourier-Reihen bzw. sie lässt sich aus dieser ableiten. Dazu werden die einzelnen Werte  ,
, ,
, des zu untersuchenden diskreten und endlichen Signals
des zu untersuchenden diskreten und endlichen Signals  als äquidistante Funktionswerte einer
als äquidistante Funktionswerte einer  -periodischen Funktion
-periodischen Funktion  angesehen:
angesehen:
 mit
mit 
Für eine solche  -periodischen Funktion f lässt sich eine Fourier-Reihe entwickeln und die Fourier-Koeffizienten lassen sich wie bereits erwähnt durch folgendes Integral berechnen:
-periodischen Funktion f lässt sich eine Fourier-Reihe entwickeln und die Fourier-Koeffizienten lassen sich wie bereits erwähnt durch folgendes Integral berechnen:
 ,
,

Dabei können die Grenzen des Integrals auch verschoben werden. Wichtig ist nur, dass über eine komplette Periodendauer integriert wird. Die Koeffizienten können also auch folgendermaßen berechnet werden:
 ,
,

Hierbei sind die Frequenzen  ein Vielfaches der Grundfrequenz:
ein Vielfaches der Grundfrequenz:

Im Fall der DFT sind allerdings nicht alle kontinuierlichen Funktionswerte bekannt, sondern nur die diskreten Messwerte  . Das bedeutet, dass sich dieses Integral nicht berechnen lässt. Daher wird das Integral durch eine Riemann-Summe genähert: Die Funktion
. Das bedeutet, dass sich dieses Integral nicht berechnen lässt. Daher wird das Integral durch eine Riemann-Summe genähert: Die Funktion  wird an den Stützstellen
wird an den Stützstellen  ausgewertet, mit der Differenz zwischen zwei Stützstellen
ausgewertet, mit der Differenz zwischen zwei Stützstellen  multipliziert und dieses Produkt wird über den Laufindex k aufsummiert. Es ergibt sich die folgende Riemann-Summe:
multipliziert und dieses Produkt wird über den Laufindex k aufsummiert. Es ergibt sich die folgende Riemann-Summe:


Dies entspricht gerade der Berechnungsformel des n-ten Koeffizienten  der Diskreten Fourier Transformierten
der Diskreten Fourier Transformierten  des Vektors
des Vektors  .
.
Betrachtet man die Berechnungsformel des Koeffizienten  , so fällt auf, dass dieser dem Koeffizienten
, so fällt auf, dass dieser dem Koeffizienten  entspricht, weshalb die diskrete Fourier-Transformierte nur zwischen
entspricht, weshalb die diskrete Fourier-Transformierte nur zwischen  und
und  definiert ist:
definiert ist:


Von der kontinuierlichen zur Diskreten Fourier Transformation
Auch zur kontinuierlichen Fourier-Transformation besitzt die DFT große Ähnlichkeiten. Um das deutlich zu machen wird eine nichtperiodische Funktion  betrachtet, die außerhalb des Intervalls
betrachtet, die außerhalb des Intervalls ![Rendered by QuickLaTeX.com [0,\ T]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2b59ae00ed207d787d5a055ada7e0a72_l3.png) verschwindet und auf diesem im Abstand
verschwindet und auf diesem im Abstand  jeweils als Funktionswert einen Eintrag aus
jeweils als Funktionswert einen Eintrag aus  annimmt:
annimmt:
 , für
, für 
Sei nun die Zahl der untersuchten Werte N deutlich größer als die Länge des gewählten Intervalls ![Rendered by QuickLaTeX.com [0,\ T]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2b59ae00ed207d787d5a055ada7e0a72_l3.png) , so lässt sich dort das Integral der Fourier-Transformierten
, so lässt sich dort das Integral der Fourier-Transformierten  der Funktion f sinnvoll durch eine diskrete Summe nähern:
der Funktion f sinnvoll durch eine diskrete Summe nähern:


Wird diese Summe nur für  berechnet, so ergibt sich:
berechnet, so ergibt sich:

Das entspricht bis auf den konstanten Faktor T der Berechnungsformel des n-ten Eintrags  der Diskreten Fourier Transformierten
der Diskreten Fourier Transformierten  .
.
IDFT: Inverse Diskrete Fourier Transformation
Um zur Formel der Inversen DFT zu gelangen, kann die Fourier-Reihe ![Rendered by QuickLaTeX.com \mathfrak{F}[f]t](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f908349dbfdc218626722d5c23e894c9_l3.png) derselben periodischen Funktion
derselben periodischen Funktion  betrachtet werden, welche oben beschrieben wurde.
betrachtet werden, welche oben beschrieben wurde.
=\sum_{n = -\infty}^{\infty} {c_n\cdot e}^{i\cdot\omega_n\cdot t}}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0469602cbb21e4286604174bf2efb90c_l3.png)
Im Fall der Diskreten Fourier Transformation werden die Koeffizienten  durch die Einträge
durch die Einträge  der Diskreten Fourier Transformierten repräsentiert. Da diese nur für
der Diskreten Fourier Transformierten repräsentiert. Da diese nur für  definiert sind, läuft der Index in der Summe auch nur zwischen diesen beiden Grenzen. Berechnet man dementsprechend diese Reihe für die Werte
definiert sind, läuft der Index in der Summe auch nur zwischen diesen beiden Grenzen. Berechnet man dementsprechend diese Reihe für die Werte  und für die Frequenzen
und für die Frequenzen  , so erhält man folgendes Ergebnis:
, so erhält man folgendes Ergebnis:
![Rendered by QuickLaTeX.com \mathfrak{F}\left[f\right]\left(k\cdot\frac{T}{N}\right)=\sum_{n=0}^{N-1}{\hat{a}}_n\cdot e^{i\cdot n\cdot\frac{2\pi}{T}\cdot k\cdot\frac{T}{N}}=\sum_{n=0}^{N-1}{\hat{a}}_n\cdot e^{2\pi i\cdot\frac{k\cdot n}{N}}=:a_k](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d703caa1218533764959f081a9ce825b_l3.png)
Definition: IDFT
Somit berechnen sich die Koeffizienten  der Inversen Diskreten Fourier Transformierten
der Inversen Diskreten Fourier Transformierten  von
von  nach Umbenennung der Indizes auf folgende Art:
nach Umbenennung der Indizes auf folgende Art:

Zur Zusammenfassung: Die Koeffizienten  der Diskreten Fourier Transformierten
der Diskreten Fourier Transformierten  von
von  lauten:
lauten:

Für den Vorfaktor  bei der Diskreten Fourier Transformation gibt es unterschiedliche Konventionen. Manchmal wird er auch bei der Inversen DFT statt bei der DFT eingefügt.
bei der Diskreten Fourier Transformation gibt es unterschiedliche Konventionen. Manchmal wird er auch bei der Inversen DFT statt bei der DFT eingefügt.
Überblick Fourier Analysis
Da nun die Diskrete Fourier Transforamtion und auch ihre Inverse bekannt sind, sollen beide noch einmal in den Kontext der Fourier-Analysis eingeordnet werden und ein kurzer Überblick über die drei wichtigsten Transformationen aus diesem Bereich gegeben werden. Dabei werden nun die in der Signalverarbeitung üblichen Bezeichnungen angewandt. Mit x soll ein Signal im Zeitbereich bezeichnet werden und mit X wird das entsprechende Signal im Frequenzbereich symbolisiert.
DFT Matrix
Wird die Abkürzung  für die N-te Einheitswurzel eingeführt, so lauten die Formeln der Diskreten Fourier Transformation:
für die N-te Einheitswurzel eingeführt, so lauten die Formeln der Diskreten Fourier Transformation:
 DFT
DFT
 IDFT
IDFT
Im Folgenden werden die einzelnen Komponenten der DFT einmal ausgeschrieben:





Dies lässt sich auch in Matrix-Schreibweise notieren:

Die dort auftretende Matrix

wird als DFT-Matrix oder Fourier-Matrix bezeichnet. Es lässt sich zeigen, dass für ihre Inverse folgender Zusammenhang gilt:
 ,
,
wobei  die komplex konjugierte Matrix von Z beschreibt.
die komplex konjugierte Matrix von Z beschreibt.
Somit lauten die Formeln der DFT und der IDFT:
 DFT
DFT
 IDFT
IDFT
Eigenschaften der DFT
Folgende Eigenschaft der DFT wurde bereits gezeigt. Würde der Koeffizient  berechnet werden, entspräche dieser dem Koeffizienten
berechnet werden, entspräche dieser dem Koeffizienten  der Diskreten Fourier Transformierten:
der Diskreten Fourier Transformierten:

Des Weiteren gewinnt man mit der DFT nur Informationen für die Frequenzen  mit
mit  . Es gilt nämlich:
. Es gilt nämlich:


Werden demnach Werte einer Signalfunktion  mit
mit  im Abstand
im Abstand  , also mit der Abtastfrequenz
, also mit der Abtastfrequenz  ermittelt, so liefert die Diskrete Fourier Transformation nur Informationen zum Frequenzspektrum der Funktion für Frequenzen, die unter
ermittelt, so liefert die Diskrete Fourier Transformation nur Informationen zum Frequenzspektrum der Funktion für Frequenzen, die unter  liegen.
liegen.
Abtasttheorem
Diese Erkenntnis wird im Abtasttheorem von Shannon zusammengefasst:
Sei  ein Signal, in dessen Frequenzspektrum
ein Signal, in dessen Frequenzspektrum  die höchste auftretende Frequenz ist. Dann ist dieses Signal vollständig durch seine Abtastwerte bestimmt, falls die Abtastfrequenz
die höchste auftretende Frequenz ist. Dann ist dieses Signal vollständig durch seine Abtastwerte bestimmt, falls die Abtastfrequenz  größer als
größer als  ist. Die Frequenz
ist. Die Frequenz  wird auch als Nyquist-Frequenz bezeichnet.
wird auch als Nyquist-Frequenz bezeichnet.
Linearität der DFT
Eine weitere leicht zu zeigende Eigenschaft der Diskreten Fourier Transformation ist die Linearität:


Diskrete Fourier Transformation Beispiel
In diesem Beispiel soll das Signal  betrachtet werden und zu den Zeiten
betrachtet werden und zu den Zeiten  und
und  abgetastet werden.
abgetastet werden.
Die DFT ist also für den Vektor  mit
mit  und
und  durchzuführen. Der Vektor lautet somit:
durchzuführen. Der Vektor lautet somit:

Mit der Formel für die DFT berechnet sich die Diskrete Fourier Transformierte mit  wie folgt:
wie folgt:




Die Diskrete Fourier Transformierte des Vektors  lautet also:
lautet also:

Das Ergebnis lässt sich auch mithilfe der Fourier-Matrix berechnen. Das sieht dann folgendermaßen aus:

Werden die passenden Werte eingesetzt, erhält man:


