Wann benutzt man das Quotientenkriterium?

Das Quotientenkriterium benutzt du vor allem dann, wenn sich der Quotient leicht vereinfachen lässt, zum Beispiel bei Fakultäten, Potenzen oder Produkten. Wenn das Quotientenkriterium eindeutig Konvergenz oder Divergenz zeigt, liefert das Wurzelkriterium dasselbe Ergebnis.

Was macht man, wenn beim Wurzelkriterium α = 1 herauskommt?

Beim Wurzelkriterium bedeutet , dass du mit diesem Kriterium nicht entscheiden kannst, ob die Reihe konvergiert oder divergiert. Dann musst du ein anderes Konvergenzkriterium verwenden, zum Beispiel einen Vergleich mit einer bekannten Reihe oder ein Kriterium, das speziell zu deiner Reihenform passt.

Gilt das Wurzelkriterium auch für Reihen mit negativen oder wechselnden Vorzeichen?

Das Wurzelkriterium gilt auch für Reihen mit negativen oder wechselnden Vorzeichen, weil du dabei mit rechnest. Wenn ist, konvergiert die Reihe sogar absolut und damit auch „normal“. Wenn ist, divergiert die Reihe unabhängig vom Vorzeichenwechsel.

Video

Wurzelkriterium

Wichtige Inhalte in diesem Video

Wurzelkriterium einfach erklärt

(00:11)

Wurzelkriterium Schritt für Schritt

(00:55)

Wurzelkriterium Beispiel

(01:58)

Das Wurzelkriterium ist eine Methode, um die Konvergenz oder Divergenz von Reihen zu bestimmen. Wie genau, erfährst du in diesem Beitrag. Unser Video zum Wurzelkriterium zeigt dir das Wichtigste dazu in kurzer Zeit.

Inhaltsübersicht

Wurzelkriterium einfach erklärt

im Videozur Stelle im Video springen

(00:11)

Du hast eine Reihe der Form

$\sum \limits_{n=0}^\infty \textcolor{red}{a_n}$

gegeben und sollst nun bestimmen, ob diese konvergiert oder divergiert? Dazu berechnest du zunächst

$\textcolor{blue}{\alpha} = \lim\limits_{n\to\infty} \sqrt[n]{\left\lvert \textcolor{red}{a_n} \right\rvert} = \lim\limits_{n\to\infty} \left\lvert \textcolor{red}{a_n} \right\rvert^{\frac{1}{n}}.$

Dann gilt

$\textcolor{blue}{\alpha} < 1 \longrightarrow$ Reihe konvergiert,

$\textcolor{blue}{\alpha} > 1 \longrightarrow$ Reihe divergiert und

$\textcolor{blue}{\alpha} = 1 \longrightarrow$ keine eindeutige Aussage möglich.

Die Kernidee hinter dem Wurzelkriterium ist ein Vergleich mit der geometrischen Reihe .

Wurzelkriterium Schritt für Schritt

im Videozur Stelle im Video springen

(00:55)

Schauen wir uns an einem konkreten Beispiel an, wie du das Wurzelkriterium Schritt-für-Schritt anwenden kannst. Dazu betrachten wir die folgende Reihe

$\sum \limits_{n=1}^\infty \frac{n^n}{4^{1 + 3n}}.$

Wir haben also

$\textcolor{red}{a_n} = \frac{n^n}{4^{1 + 3n}}.$

Schritt 1: Zuerst nimmst du den Betrag von $\textcolor{red}{a_n}$

$\left\lvert \textcolor{red}{a_n} \right\rvert = \left\lvert \frac{n^n}{4^{1 + 3n}} \right\rvert.$

Schritt 2: Davon ziehst du dann die -te Wurzel

$\left\lvert \textcolor{red}{a_n} \right\rvert^{\frac{1}{n}} = \left\lvert \frac{n^n}{4^{1 + 3n}} \right\rvert^{\frac{1}{n}}.$

Der Bruch

$\frac{n^n}{4^{1 + 3n}}$

ist für alle eine positive Zahl. Daher kannst du die Betragsstriche weglassen

$\left\lvert \frac{n^n}{4^{1 + 3n}} \right\rvert^{\frac{1}{n}} = \left(\frac{n^n}{4^{1 + 3n}}\right)^{\frac{1}{n}} = \frac{n}{4^{\frac{1}{n} + 3}} = \frac{n}{4^3 \cdot 4^{\frac{1}{n}}}.$

Schritt 3: Nun berechnest du den Grenzwert für $n\to\infty$

$\textcolor{blue}{\alpha} = \lim\limits_{n\to\infty} \left\lvert \textcolor{red}{a_n} \right\rvert^{\frac{1}{n}} = \lim\limits_{n\to\infty} \frac{n}{4^3 \cdot 4^{\frac{1}{n}}} = \frac{1}{4^3} \lim\limits_{n\to\infty} \frac{n}{4^{\frac{1}{n}}} = \infty.$

Dabei nutzt du aus, dass gilt

$\lim\limits_{n\to\infty} 4^{\frac{1}{n}} = 1.$

Schritt 4: Somit hast du

$\textcolor{blue}{\alpha} > 1$

und die Reihe

$\sum \limits_{n=1}^\infty \frac{n^n}{4^{1 + 3n}}$

divergiert folglich nach dem Wurzelkriterium.

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Wurzelkriterium Beispiel

im Videozur Stelle im Video springen

(01:58)

Wenden wir das Wurzelkriterium auf ein weiteres Beispiel an. Nehmen wir an, dass du folgende Reihe gegeben hast

$\sum \limits_{n=0}^\infty \left(\frac{3n + 2n^2 - 4n^3}{9n^3 + 12}\right)^n.$

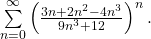
Schritt 1: Du bildest zuerst wieder den Betrag der Reihenglieder a_n

$\left\lvert \left(\frac{3n + 2n^2 - 4n^3}{9n^3 + 12}\right)^n \right\rvert.$

Schritt 2: Davon ziehst du dann die -te Wurzel

$\left\lvert \left(\frac{3n + 2n^2 - 4n^3}{9n^3 + 12}\right)^n \right\rvert^{\frac{1}{n}}.$

Diesen Ausdruck kannst du als nächstes etwas vereinfachen

$\left\lvert \left(\frac{3n + 2n^2 - 4n^3}{9n^3 + 12}\right) \right\rvert.$

Schritt 3: Nun berechnest du den Grenzwert für $n\to\infty$

$\textcolor{blue}{\alpha} = \lim\limits_{n\to\infty} \left\lvert \left(\frac{3n + 2n^2 - 4n^3}{9n^3 + 12}\right) \right\rvert = \left\lvert\frac{-4}{9}\right\rvert = \frac{4}{9} < 1.$

Schritt 4: Es gilt also

$\textcolor{blue}{\alpha} < 1$

und damit konvergiert die Reihe

$\sum \limits_{n=0}^\infty \left(\frac{3n + 2n^2 - 4n^3}{9n^3 + 12}\right)^n.$

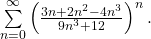
Wurzelkriterium vs. Quotientenkriterium

Neben dem Wurzelkriterium als Methode zum Untersuchen des Konvergenzverhaltens von Reihen gibt es auch das Quotientenkriterium. Beide sind sich in der Tatsache ähnlich, dass ein bestimmter Grenzwert $\alpha$ berechnet werden soll. Auch die Fälle

$\alpha < 1, \alpha > 1$ und $\alpha = 1$

werden auf ähnliche Weise unterschieden. Das hat unter anderem damit zu tun, dass beide Kriterien auf den Vergleich zur geometrischen Reihe beruhen.

Wenn das Quotientenkriterium eine Reihe als konvergent ( $\alpha < 1$ ) oder divergent ( $\alpha > 1$ ) einstuft, so auch das Wurzelkriterium. Nun könnte es aber sein, dass du durch das Wurzelkriterium keine eindeutige Aussage erhältst (also $\alpha = 1$ ). Dann wird dir das Quotientenkriterium nicht weiterhelfen können.

Umgekehrt, gibt dir das Quotientenkriterium keine eindeutige Aussage, dann könnte dir das Wurzelkriterium dennoch weiterhelfen.

Wurzelkriterium Beweis

In diesem Abschnitt geben wir dir einen Beweis für die Fälle $\alpha < 1$ und $\alpha > 1$ .

Beweis für $\alpha < 1$

Wir haben $\alpha < 1$ und wollen zeigen, dass dann die Reihe $\sum \limits_{n=1}^\infty a_n$ konvergiert. Wenn $\alpha < 1$ ist, dann können wir ein $\beta < 1$ finden, sodass gilt $\alpha < \beta < 1.$ Jetzt wissen wir, dass $\alpha$ der Grenzwert

$\alpha = \lim\limits_{n\to\infty} \left\lvert a_n \right\rvert^{\frac{1}{n}}$

ist. Da nun $\alpha < \beta$ gilt, gibt es eine natürliche Zahl , sodass $\left\lvert a_n \right\rvert^{\frac{1}{n}} < \beta$ gilt für alle $n \geq N$ . Diese Ungleichung können wir umformen

$\left\lvert a_n \right\rvert < \beta^n$ für $n \geq N$ .

Nun ist

$\sum \limits_{n=0}^\infty \beta^n$

eine geometrische Reihe und da $\beta < 1$ ist, konvergiert diese. Nach dem Majorantenkriterium konvergiert daher auch die Reihe

$\sum \limits_{n=1}^\infty a_n$ .

Wurzelkriterium Beweis Teil 1, Wurzelkriterium Beweis, Wurzelkriterium Konvergenz Folge, Wurzelkriterium Konvergenz Beweis, Wurzelkriterium Konvergenz — Wurzelkriterium Beweis Teil 1.

Beweis für $\alpha > 1$

Es sei $\alpha > 1$ . Wir wollen zeigen, dass dann die Reihe $\sum \limits_{n=1}^\infty a_n$ divergiert. Da $\alpha$ der Grenzwert

$\alpha = \lim\limits_{n\to\infty} \left\lvert a_n \right\rvert^{\frac{1}{n}}$

ist, gibt es eine natürliche Zahl , sodass für alle $n \geq N$ gilt $\left\lvert a_n \right\rvert^{\frac{1}{n}} > 1$ oder umgeformt $\left\lvert a_n \right\rvert > 1^n = 1.$

Das bedeutet aber, dass dann

$\lim\limits_{n\to\infty} \left\lvert a_n \right\rvert \neq 0$

gilt und somit auch

$\lim\limits_{n\to\infty} a_n \neq 0.$

Damit bildet die Folge der Reihenglieder keine Nullfolge und nach dem Nullfolgenkriterium divergiert daher die Reihe

$\sum \limits_{n=1}^\infty a_n,$

was zu zeigen war.

Wurzelkriterium Beweis Teil 2, Wurzelkriterium Beweis, Wurzelkriterium Konvergenz Folge, Wurzelkriterium Divergenz Beweis, Wurzelkriterium Divergenz — Wurzelkriterium Beweis Teil 2.

Wurzelkriterium Beispielaufgabe

Du hast die folgende Reihe gegeben

$\sum \limits_{n=5}^\infty \frac{(-15)^n}{n}.$

Untersuche das Konvergenzverhalten dieser Reihe.

Lösung

Wir haben

$\textcolor{red}{a_n} = \frac{(-15)^n}{n}.$

Im ersten Schritt bilden wir davon den Betrag und ziehen die -te Wurzel

$\left\lvert \textcolor{red}{a_n} \right\rvert^{\frac{1}{n}} = \left\lvert \frac{(-15)^n}{n} \right\rvert^{\frac{1}{n}} = \left\lvert \frac{-15}{n^{\frac{1}{n}}} \right\rvert = \frac{15}{n^{\frac{1}{n}}}.$

Nun berechnen wir den Grenzwert für $n\to\infty$

$\textcolor{blue}{\alpha} = \lim\limits_{n\to\infty} \left\lvert \textcolor{red}{a_n} \right\rvert^{\frac{1}{n}} = \lim\limits_{n\to\infty} \frac{15}{n^{\frac{1}{n}}} = 15 > 1.$

Wir haben hier die Tatsache ausgenutzt, dass

$\lim\limits_{n\to\infty} n^{\frac{1}{n}} = 1$

gilt. Somit haben wir

$\textcolor{blue}{\alpha} > 1$

und die Reihe

$\sum \limits_{n=5}^\infty \frac{(-15)^n}{n}$

divergiert.

Hinweis: Lass dich nicht dadurch irritieren, dass die Reihe erst bei n = 5 beginnt. Wenn du die Konvergenz von Reihen untersuchst, spielt es keine Rolle, was für ein Verhalten endlich viele Reihenglieder besitzen. Du würdest also das gleiche Ergebnis erhalten, wenn die Reihe stattdessen bei n = 1 beginnen würde. Der Fall n = 0 ist nicht möglich, da du ansonsten durch Null teilen würdest.

Wurzelkriterium — häufigste Fragen

(ausklappen)

Wann benutzt man das Quotientenkriterium?

Das Quotientenkriterium benutzt du vor allem dann, wenn sich der Quotient $a_{n+1}/a_n$ leicht vereinfachen lässt, zum Beispiel bei Fakultäten, Potenzen oder Produkten. Wenn das Quotientenkriterium eindeutig Konvergenz oder Divergenz zeigt, liefert das Wurzelkriterium dasselbe Ergebnis.
Was macht man, wenn beim Wurzelkriterium α = 1 herauskommt?

Beim Wurzelkriterium bedeutet $\alpha = 1$ , dass du mit diesem Kriterium nicht entscheiden kannst, ob die Reihe konvergiert oder divergiert. Dann musst du ein anderes Konvergenzkriterium verwenden, zum Beispiel einen Vergleich mit einer bekannten Reihe oder ein Kriterium, das speziell zu deiner Reihenform passt.
Gilt das Wurzelkriterium auch für Reihen mit negativen oder wechselnden Vorzeichen?

Das Wurzelkriterium gilt auch für Reihen mit negativen oder wechselnden Vorzeichen, weil du dabei mit rechnest. Wenn $\alpha < 1$ ist, konvergiert die Reihe sogar absolut und damit auch „normal“. Wenn $\alpha > 1$ ist, divergiert die Reihe unabhängig vom Vorzeichenwechsel.