Flächeninhalt Viereck
In der Geometrie gibt es viele verschiedene Arten von Vierecken. Wie du den Flächeninhalt von Vierecken bestimmst, zeigen wir dir in unserem Beitrag und im Video.
Inhaltsübersicht
Flächeninhalt Viereck — Übersicht
Hier findest du eine Übersicht der Formeln zur Berechnung des Flächeninhalts verschiedener Vierecke:
| Vierecktyp | Formel | Erklärung |
| Quadrat | a • a | Seitenlänge a mit sich selbst multiplizieren |
| Rechteck | a • b | Länge a mal Breite b |
| Parallelogramm | a • h | Basis a mal Höhe h |
| Trapez |  |
Summe der beiden parallelen Seiten (a und b) mal Höhe h, dann geteilt durch 2 |
| Drachenviereck |  |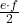
Diagonalen e und f miteinander multiplizieren und durch 2 teilen |
Quadrate und Rechtecke
Bei einem Quadrat sind alle vier Seiten gleich lang. Deshalb bezeichnest du alle Seiten mit einem a. Es hat außerdem vier rechte Winkel. Für die Berechnung der Fläche eines Quadrats nutzt du die Formel:
A = a • a
Ein Rechteck hat ebenfalls vier rechte Winkel, aber die gegenüberliegenden Seiten a und b sind jeweils gleich lang. Hier verwendest du die Formel:
A = a • b
Beispiel:
Wenn die Seitenlänge a eines Quadrats 5 cm beträgt, dann ist die Fläche A:
A = 5 cm • 5 cm = 25 cm²
Du hast ein Rechteck mit einer Länge a von 8 cm und einer Breite b von 3 cm gegeben. Die Fläche A ist dann:
A = 8 cm • 3 cm = 24 cm²
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Parallelogramme
Ein Parallelogramm erkennst du daran, dass es ein Viereck, ist, bei dem die gegenüberliegenden Seiten parallel und gleich lang sind. Die gegenüberliegenden Winkel sind ebenfalls gleich. Um die Fläche eines Parallelogramms zu berechnen, nutzt du die Formel:
A = a • h
Dabei ist a die Länge der Grundseite und h die Höhe des Parallelogramms.
Beispiel:
Wenn die Grundseite a eines Parallelogramms 6 cm beträgt und die Höhe h 4 cm ist, berechnest du die Fläche so:
A = 6 cm • 4 cm = 24 cm²
Trapeze
Trapeze sind Vierecke mit mindestens einem Paar paralleler Seiten. Die parallelen Seiten nennst du Grundseiten und bezeichnest sie mit a und c. Die Höhe h ist der Abstand zwischen den beiden Grundseiten. Du berechnest die Fläche eines Trapezes mit der Formel:
A = 
Beispiel:
Zum Beispiel hast du ein Trapez mit den Grundseiten a und c, die 6 cm und 4 cm lang sind und der Höhe h, die 5 cm beträgt, gegeben. Die Fläche berechnest du dann so:
A = 
= 25 cm²
Drachenvierecke
Ein besonderes Viereck ist das Drachenviereck. Es hat zwei Paare von benachbarten Seiten, die gleich lang sind. Die Diagonalen e und f stehen dabei senkrecht aufeinander. Zur Berechnung der Fläche eines Drachenvierecks brauchst du die Formel:
A = 
Beispiel:
Wenn die Diagonalen e und f eines Drachenvierecks 8 cm und 6 cm lang sind, dann ist die Fläche:
A = 
= 24 cm²
Flächeninhalt Viereck — häufigste Fragen
(ausklappen)
Flächeninhalt Viereck — häufigste Fragen
(ausklappen)-
Wie berechnet man den Flächeninhalt eines Vierecks? Die Berechnung der Fläche eines Vierecks hängt von der Art des Vierecks ab. Für Quadrate und Rechtecke nutzt du die Formel A = a • b. Für Parallelogramme nutzt du A = a • h, für Trapeze A = (a + b) • h • 0,5 und für Drachenvierecke A = e • f • 0,5
-
Wie berechnet man den Flächeninhalt von Rechtecken? Um den Flächeninhalt A eines Rechtecks zu berechnen, multiplizierst du die Länge a mit der Breite b. Also: A = a • b.
Flächeninhalt Dreieck
Jetzt weißt du, wie du den Flächeninhalt verschiedener Vierecke ausrechnest. Wenn du wissen willst, wie du bei der Berechnung des Flächeninhalts von Dreiecken vorgehst, dann schau dir gleich unser Video dazu an!
