Inkreis und Umkreis Dreieck
Du möchtest wissen, was der Inkreis und der Umkreis eines Dreiecks sind und wie man sie konstruiert? Hier und im Video zeigen wir dir alles, was du wissen musst!
Inhaltsübersicht
Inkreis und Umkreis eines Dreiecks einfach erklärt
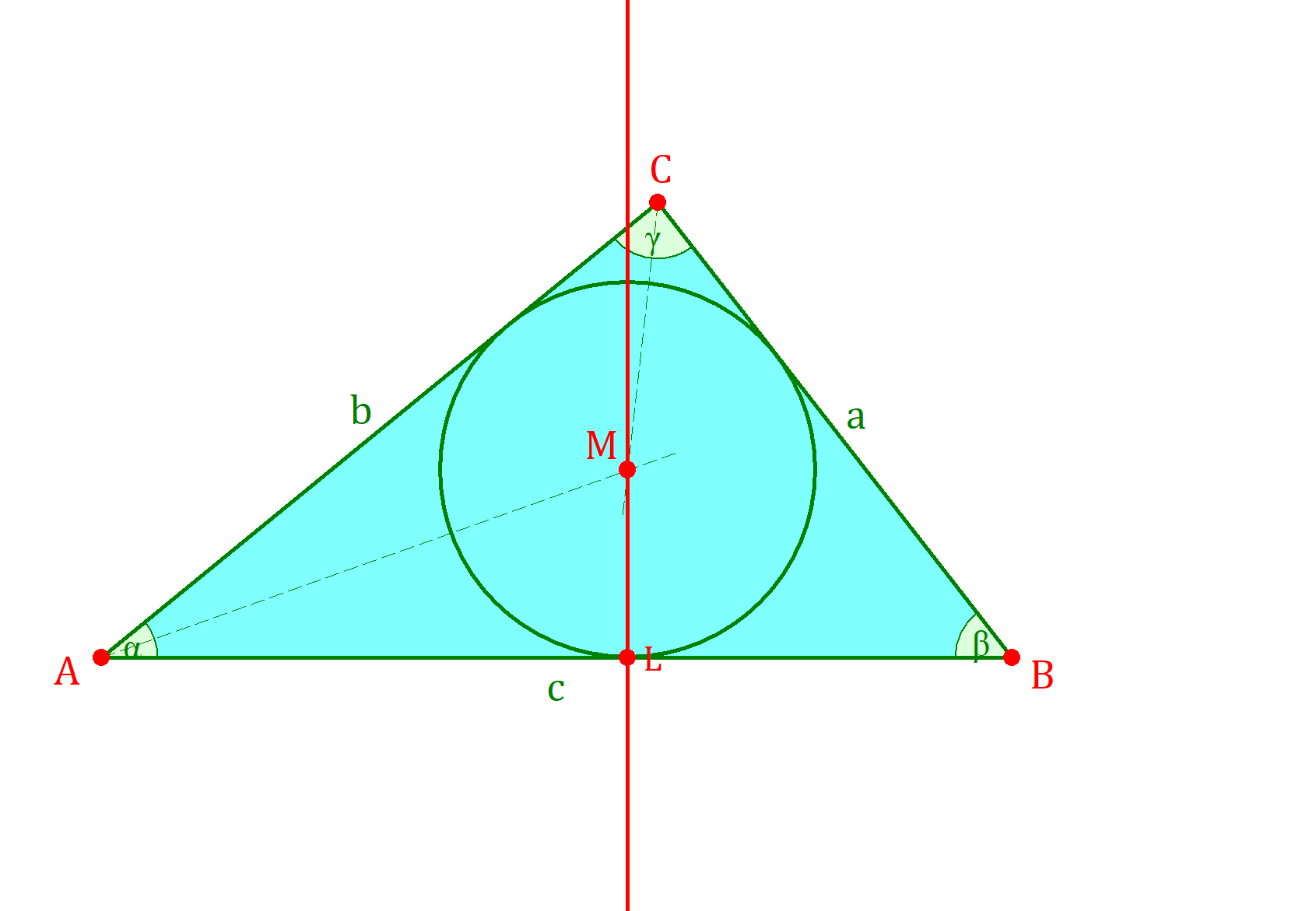
Der Inkreis liegt im Inneren des Dreiecks und berührt jede Seite genau einmal, ohne sie zu schneiden. Alle Dreiecksseiten sind also Tangenten des Inkreises. Sein Mittelpunkt ist dabei der Schnittpunkt der drei Winkelhalbierenden.
Der Umkreis liegt dagegen außerhalb des Dreiecks. Dabei berührt er alle drei Eckpunkte des Dreiecks. Sein Mittelpunkt ist der Schnittpunkt der drei Mittelsenkrechten.
Als Nächstes zeigen wir dir, wie du einen Inkreis und einen Umkreis selbst konstruieren kannst. Fangen wir mit dem Inkreis an.
Inkreis konstruieren
-
Mittelpunkt bestimmen:
Um den Inkreis eines Dreiecks zeichnen zu können, musst du seinen Mittelpunkt herausfinden. Er ist der Schnittpunkt der Winkelhalbierenden.Der erste Schritt ist daher das Bestimmen der Winkelhalbierenden. Da sich alle drei denselben Schnittpunkt teilen, reicht es schon aus, zwei von ihnen zu einzuzeichnen. Wie das geht, zeigen wir dir in unserem Beitrag zu Winkelhalbierenden. Danach kannst du ganz einfach den Schnittpunkt ablesen und als Mittelpunkt M markieren.
Schnittpunkt der Winkelhalbierenden bestimmen -
Radius bestimmen:
Im nächsten Schritt bestimmst du den Radius des Inkreises. Dafür ziehst du eine gerade Linie, die im rechten Winkel auf einer Seite steht. Achte dabei darauf, dass die Linie auch durch den Mittelpunkt M geht. Der daraus folgende Schnittpunkt mit der Seite des Dreiecks ist der Lotfußpunkt L. Der Abstand zwischen L und M ist der Radius deines Inkreises. Gut zu wissen: Eine Gerade, die senkrecht, also im rechten Winkel zu einer anderen Geraden steht, nennst du auch Lot. Das Einzeichnen des Lots wird auch als „Lot fällen“ bezeichnet. Sein Schnittpunkt mit der Geraden ist der Lotfußpunkt.
Lot einzeichne -
Inkreis einzeichnen:
Jetzt kannst du mithilfe von Mittelpunkt und Radius den Inkreis einzeichnen. Dazu setzt du deinen Zirkel an den Mittelpunkt M an und fährst durch den Lotfußpunkt L.
- Zwei Winkelhalbierende einzeichnen und Schnittpunkt bestimmen.
→ Mittelpunkt des Inkreises. - Lot durch Dreiecksseite und Mittelpunkt fällen und Lotfußpunkt bestimmen.
- Mit Zirkel den Inkreis ausgehend vom Mittelpunkt durch den Lotfußpunkt ziehen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Umkreis konstruieren
Für einen Umkreis verläuft die Konstruktion sehr ähnlich wie bei einem Inkreis. Anstelle der Winkelhalbierenden, musst du jedoch die Mittelsenkrechten der Seiten des Dreiecks bestimmen.
-
Mittelpunkt bestimmen:
Um den Mittelpunkt des Umkreises herauszufinden, musst du im ersten Schritt die Mittelsenkrechten bestimmen. Da sich hier wieder alle drei einen Schnittpunkt teilen, reicht es zwei von ihnen zu einzuzeichnen. Dabei kann dir unser Beitrag zu Mittelsenkrechten helfen. Anschließend kannst du einfach den Schnittpunkt ablesen und als Mittelpunkt M markieren.
Mittelsenkrechte einzeichnen -
Radius bestimmen & Umkreis einzeichnen:
Jetzt fehlt noch der Radius des Umkreises. Er ist der Abstand zwischen dem Mittelpunkt M und einer beliebigen Ecke des Dreiecks. Indem du den Zirkel am Mittelpunkt M ansetzt und ihn durch die Ecken des Dreiecks fährst, zeichnest du den fertigen Umkreis ein.
- Zwei Mittelsenkrechten einzeichnen und Schnittpunkt bestimmen.
→ Mittelpunkt des Umkreises. - Mit Zirkel den Umkreis ausgehend vom Mittelpunkt durch die Eckpunkte ziehen.
Inkreis und Umkreis Dreieck — häufigste Fragen
(ausklappen)
Inkreis und Umkreis Dreieck — häufigste Fragen
(ausklappen)-
Warum schneiden sich alle Winkelhalbierenden in einem Punkt im Dreieck?Alle Winkelhalbierenden schneiden sich in einem Punkt, weil jeder Punkt auf einer Winkelhalbierenden zu den beiden Schenkeln dieses Winkels den gleichen Abstand hat. Der gemeinsame Schnittpunkt hat deshalb zu allen drei Dreiecksseiten den gleichen Abstand. Genau dieser Punkt ist der Inkreismittelpunkt.
-
Warum schneiden sich alle Mittelsenkrechten in einem Punkt im Dreieck?Alle Mittelsenkrechten schneiden sich in einem Punkt, weil jeder Punkt auf der Mittelsenkrechten einer Strecke von deren Endpunkten gleich weit entfernt ist. Der Schnittpunkt ist damit von allen drei Eckpunkten des Dreiecks gleich weit entfernt. Deshalb ist er der Umkreismittelpunkt.
-
Wo liegt der Umkreismittelpunkt bei spitzen stumpfen und rechtwinkligen Dreiecken?Der Umkreismittelpunkt liegt beim spitzwinkligen Dreieck im Inneren, beim stumpfwinkligen Dreieck außerhalb und beim rechtwinkligen Dreieck genau in der Mitte der Hypotenuse. Das folgt daraus, dass der Umkreismittelpunkt von allen Eckpunkten gleich weit entfernt sein muss.
-
Welche Fehler passieren oft beim Konstruieren von Inkreis und Umkreis?Häufige Fehler sind: Winkelhalbierende mit Seitenhalbierenden zu verwechseln und dadurch den falschen Inkreismittelpunkt zu erhalten. Außerdem wird beim Inkreis das Lot (Senkrechte) nicht durch den Mittelpunkt gezeichnet, dann ist der Radius falsch. Beim Umkreis wird oft keine echte Mittelsenkrechte konstruiert, also nicht senkrecht durch den Seitenmittelpunkt.
-
Wie prüfe ich schnell ob mein Inkreis wirklich alle Seiten berührt?Du prüfst den Inkreis schnell, indem du kontrollierst, ob der Abstand vom Inkreismittelpunkt zu jeder Dreiecksseite gleich groß ist, denn dieser Abstand ist der Radius. Konkret: Fällt von M auf jede Seite ein Lot und miss die drei Lotstrecken; sind sie gleich lang, berührt der Kreis alle Seiten.
Flächeninhalt Kreis
Sehr gut! Jetzt weißt du, was du unter einem Inkreis und einem Umkreis verstehst und wie du sie konstruieren kannst. Wie du im nächsten Schritt den Flächeninhalt eines Kreises berechnen kannst, zeigen wir dir hier.