Wie erkenne ich, ob eine Aufgabe wirklich ein regelmäßiger Tetraeder ist?

Du erkennst einen regelmäßigen Tetraeder daran, dass alle 6 Kanten gleich lang sind und alle 4 Flächen kongruente gleichseitige Dreiecke sind. Dann sind auch alle Winkel und Kantenbeziehungen symmetrisch. Beispiel: Steht „alle Kanten haben Länge a“, ist es ein regelmäßiger Tetraeder.

Wie berechne ich die Oberfläche eines Tetraeders, wenn nur die Höhe gegeben ist?

Die Oberfläche eines regelmäßigen Tetraeders lässt sich aus der Höhe berechnen, indem du zuerst die Kantenlänge bestimmst: Aus folgt . Danach setzt du in ein und erhältst .

Wie berechne ich das Volumen eines Tetraeders, wenn nur die Oberfläche gegeben ist?

Das Volumen eines regelmäßigen Tetraeders aus der Oberfläche bekommst du, indem du zuerst aus berechnest: . Dann setzt du in ein, also .

Welche Fehler passieren oft beim Umformen der Wurzeln in der Volumenformel?

Häufige Fehler beim Umformen sind falsches Zerlegen der Wurzel und falsches „Wurzelziehen“ aus Summen. Beispiel: Richtig ist , aber falsch ist . Ebenfalls falsch ist .

Warum ist die Höhe im Tetraeder nicht die Dreieckshöhe der Seitenfläche?

Die Höhe im Tetraeder ist die senkrechte Strecke von einer Ecke auf die Grundfläche, nicht die Höhe innerhalb einer Seitenfläche. Die Dreieckshöhe liegt in einer Seitenfläche und endet auf einer Kante dieser Fläche. Beispiel: Die Tetraederhöhe trifft den Schwerpunkt der Grundfläche, nicht den Mittelpunkt einer Grundkante.

Video

Quiz

Hier geht's zum Video „Kongruenz“

Hier geht's zum Video „Volumen berechnen“

Hier geht's zum Video „Oberflächeninhalt“

Hier geht's zum Video „Volumen Pyramide“

Hier geht's zum Video „Gleichseitiges Dreieck“

Hier geht's zum Video „Wurzelrechnung“

Hier geht's zum Video „Volumen Pyramide“

Tetraeder — Volumen und Oberfläche

Wichtige Inhalte in diesem Video

Tetraeder — Volumen und Oberfläche einfach erklärt

(00:15)

Volumen und Oberfläche berechnen — Beispiel

(00:57)

Formeln — Herleitung

(01:50)

Du möchtest wissen, wie du die Oberfläche und das Volumen eines Tetraeders berechnest? Dann ließ dir unseren Beitrag durch und schau in unser Video rein!

Inhaltsübersicht

Tetraeder — Volumen und Oberfläche einfach erklärt

im Videozur Stelle im Video springen

(00:15)

Ein Tetraeder ist eine spezielle Art der Pyramide, die aus vier gleichseitigen, kongruenten Dreiecken besteht. Davon ist ein Dreieck die Grundfläche und die anderen drei sind die Seitenflächen. Dadurch hat der Tetraeder vier Ecken und sechs Kanten mit der jeweils gleichen Länge a.

Volumen Tetraeder, Oberfläche Tetraeder, Tetraeder Volumen Formel, Oberflächeninhalt Tetraeder, Tetraeder Volumen, Tetraeder Oberfläche — Tetraeder

Die wichtigsten Tetraeder Formeln sind:

Oberfläche A = a² · $\sqrt{3}$
Volumen V = $\sqrt{2} \cdot \frac{\textcolor{blue}{a}^3}{12}$
Höhe h = $\sqrt{6} \cdot \frac{\textcolor{blue}{a}}{3}$

Expertenwissen zur Kongruenz

Ein Tetraeder hat vier kongruente Seitenflächen. Kongruenz bedeutet, dass zwei Figuren dieselbe Form und Größe haben. Legst du die vier Dreiecksseiten des Tetraeders übereinander, dann sind sie deckungsgleich.

Volumen und Oberfläche berechnen — Beispiel

im Videozur Stelle im Video springen

(00:57)

Berechne das Volumen (V) und die Oberfläche (A) von einem Tetraeder mit der Kantenlänge a = 5 cm.

Volumen Tetraeder berechnen: a in die Formel einsetzen und V ausrechnen

V = $\sqrt{2} \cdot \frac{\textcolor{blue}{a}^3}{12}$

V = $\sqrt{2} \cdot \frac{\textcolor{blue}{5}^3}{12}$

V ≈ 14,73 cm³
Oberflächeninhalt Tetraeder berechnen: a in die Formel einsetzen und A bestimmen

A = a² · $\sqrt{3}$

A = 5² · $\sqrt{3}$

A ≈ 43,3 cm²

Der Tetraeder mit der Kantenlänge a = 5 cm hat ein Volumen von 14,73 cm³ und eine Oberfläche von 43,3 cm².

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Formeln — Herleitung

im Videozur Stelle im Video springen

(01:50)

Wenn du dir die Formel für die Oberfläche und das Volumen eines Tetraeders herleiten möchtest, kannst du dir die folgenden Rechnungen anschauen:

Herleitung Formel Volumen:
Das Volumen eines Tetraeders lässt sich aus dem Volumen einer Pyramide herleiten, indem die Grundfläche und die Höhe mit einem Drittel multipliziert werden. Die Grundfläche eines Tetraeders ist die Fläche eines gleichseitigen Dreiecks .

V_Pyramide =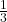 $\frac{1}{3}$ · G · h

V_Tetraeder = $\frac{1}{3} \cdot \textcolor{red}{\frac{a^2}{4} \cdot \sqrt{3}} \cdot \textcolor{cyan}{\frac{a}{3} \cdot \sqrt{6}}$

→ das kannst du nun zusammenfassen und teilweise Wurzelziehen

V = $\frac{a^3}{36}\cdot \sqrt{3 \cdot 6} = \frac{a^3}{36}\cdot \sqrt{18} = \frac{a^3}{36}\cdot \sqrt{2 \cdot 9} = \frac{a^3}{36}\cdot 3 \cdot \sqrt{2}$

V = $\sqrt{2} \cdot \frac{\textcolor{blue}{a}^3}{12}$
Herleitung Formel Oberfläche:
Die Oberfläche eines Tetraeders besteht aus vier gleichseitigen Dreiecken

A = 4 · A_Dreieck

A = $\textcolor{orange}{4} \cdot \sqrt{3} \cdot \frac{\textcolor{blue}{a}^2}{\textcolor{orange}{4}}$

→ hier kürzt sich die 4 heraus

A = a² · $\sqrt{3}$

Tetraeder — Volumen und Oberfläche — häufigste Fragen

(ausklappen)

Wie erkenne ich, ob eine Aufgabe wirklich ein regelmäßiger Tetraeder ist?

Du erkennst einen regelmäßigen Tetraeder daran, dass alle 6 Kanten gleich lang sind und alle 4 Flächen kongruente gleichseitige Dreiecke sind. Dann sind auch alle Winkel und Kantenbeziehungen symmetrisch. Beispiel: Steht „alle Kanten haben Länge a“, ist es ein regelmäßiger Tetraeder.
Wie berechne ich die Oberfläche eines Tetraeders, wenn nur die Höhe gegeben ist?

Die Oberfläche eines regelmäßigen Tetraeders lässt sich aus der Höhe berechnen, indem du zuerst die Kantenlänge bestimmst: Aus $h=\frac{\sqrt{6}}{3}a$ folgt $a=\frac{3h}{\sqrt{6}}$ . Danach setzt du in $A=a^2\sqrt{3}$ ein und erhältst $A=\frac{3\sqrt{3}}{2}h^2$ .
Wie berechne ich das Volumen eines Tetraeders, wenn nur die Oberfläche gegeben ist?

Das Volumen eines regelmäßigen Tetraeders aus der Oberfläche bekommst du, indem du zuerst aus $A=a^2\sqrt{3}$ berechnest: $a=\sqrt{\frac{A}{\sqrt{3}}}$ . Dann setzt du in $V=\frac{\sqrt{2}}{12}a^3$ ein, also $V=\frac{\sqrt{2}}{12}\left(\frac{A}{\sqrt{3}}\right)^{3/2}$ .
Welche Fehler passieren oft beim Umformen der Wurzeln in der Volumenformel?

Häufige Fehler beim Umformen sind falsches Zerlegen der Wurzel und falsches „Wurzelziehen“ aus Summen. Beispiel: Richtig ist $\sqrt{18}=\sqrt{9\cdot 2}=3\sqrt{2}$ , aber falsch ist $\sqrt{18}=9\sqrt{2}$ . Ebenfalls falsch ist $\sqrt{a+b}=\sqrt{a}+\sqrt{b}$ .
Warum ist die Höhe im Tetraeder nicht die Dreieckshöhe der Seitenfläche?

Die Höhe im Tetraeder ist die senkrechte Strecke von einer Ecke auf die Grundfläche, nicht die Höhe innerhalb einer Seitenfläche. Die Dreieckshöhe liegt in einer Seitenfläche und endet auf einer Kante dieser Fläche. Beispiel: Die Tetraederhöhe trifft den Schwerpunkt der Grundfläche, nicht den Mittelpunkt einer Grundkante.

Volumen Pyramide

Super! Du kennst dich nun mit der Berechnung von Volumen und Oberfläche eines Tetraeders aus. Möchtest du mehr über das Volumen einer Pyramide erfahren? Dann klick direkt in unser Video rein!