Mittelsenkrechte Dreieck
Du willst wissen, was eine Mittelsenkrechte in einem Dreieck ist und wie du sie konstruierst? In diesem Beitrag und im Video findest du alle wichtigen Informationen!
Inhaltsübersicht
Mittelsenkrechte Dreieck einfach erklärt
Die Mittelsenkrechte eines Dreiecks ist eine Linie, die senkrecht auf der Mitte einer Dreiecksseite steht. Da ein Dreieck drei Seiten hat, gibt es auch drei Mittelsenkrechten. Diese schneiden sich alle in genau einem Punkt M. Das besondere hierbei ist, dass die Eckpunkte A, B und C des Dreiecks alle gleich weit vom Punkt M entfernt sind.
Der Punkt M ist der Mittelpunkt des Dreiecks. Von dort aus kannst du einen Kreis um das Dreieck ziehen, der durch alle Eckpunkte geht. Diesen Kreis nennst du auch Umkreis eines Dreiecks.
Merke: Die Mittelsenkrechten der Seiten a, b und c nennst du ma, mb und mc.
Mittelsenkrechte Dreieck — Konstruktion
Die Mittelsenkrechten kannst du mithilfe eines Zirkels und der folgenden Schritt für Schritt Anleitung konstruieren.
In diesem Beispiel startest du mit der Mittelsenkrechten ma der Seite a.
-
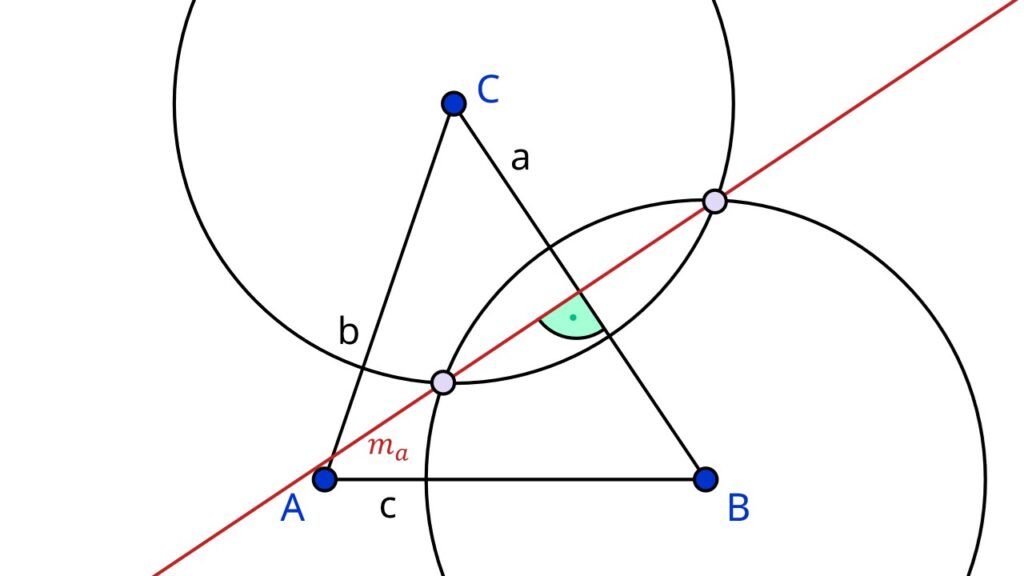
Schritt: Du setzt deine Zirkelspitze zuerst am Eckpunkt B an und zeichnest einen Halbkreis, der die Seite a schneidet. Dabei sollte der Radius deines Kreises größer als die Hälfte der Seite a sein.
Konstruktion der Mittelsenkrechte ma -
Schritt: Dasselbe machst du am Eckpunkt C mit dem gleichen Radius.
Konstruktion der Mittelsenkrechte ma -
Schritt: Die Kreise schneiden sich nun in zwei Punkten. Du nimmst dir ein Lineal und ziehst eine Linie durch die Schnittpunkte. Das ist die gesuchte Mittelsenkrechte ma, die durch den Mittelpunkt der Seite a verläuft.
Um die Mittelsenkrechten mb und mc herauszufinden, gehst du nach demselben Prinzip vor. Bei mb setzt du deinen Zirkel bei den Eckpunkten A und C an und bei mc setzt du deinen Zirkel bei den Eckpunkten A und B an. Wenn du alle Mittelsenkrechten konstruiert hast, schneiden sie sich im Punkt M.
Übrigens: Um den Punkt M zu bestimmen, brauchst du nur zwei Mittelsenkrechten. Die dritte Mittelsenkrechte kannst du konstruieren, wenn du die anderen beiden überprüfen möchtest. Das liegt daran, dass alle drei Mittelsenkrechten durch denselben Schnittpunkt verlaufen.
Der Mittelpunkt M eines Umkreises liegt bei
- rechtwinkligen Dreiecken auf der Hypotenuse.
- gleichseitigen Dreiecken auf der Symmetrieachse.
- spitzwinkligen Dreiecken innerhalb des Dreiecks.
- stumpfwinkligen Dreiecken außerhalb des Dreiecks.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Umkreis Dreieck — Konstruktion
Nachdem du die Mittelsenkrechten bestimmt hast, kannst du jetzt den Umkreis des Dreiecks konstruieren. Du brauchst auch hier einen Zirkel und den Punkt M.
Die Zirkelspitze setzt du beim Mittelpunkt M an. Der Radius ist der Abstand zwischen M und dem Eckpunkt A. Wenn du nun einen Kreis um den Mittelpunkt ziehst, liegen alle Eckpunkte auf der Kreislinie. Das ist der Umkreis eines Dreiecks.
Das Besondere dabei ist, dass alle Eckpunkte gleich weit vom Mittelpunkt M entfernt sind. Das liegt daran, weil der Radius des Kreises überall gleich ist. Da alle Eckpunkte auf dem Umkreis liegen, haben sie somit alle den gleichen Abstand zum Mittelpunkt M.
Übrigens: Dadurch, dass alle Eckpunkte gleich weit vom Mittelpunkt M entfernt sind, kannst als Radius auch den Abstand zwischen dem Mittelpunkt M und dem Eckpunkt B oder C nehmen.
Wo begegnet dir der Umkreis im Alltag?
Du möchtest zum Beispiel wissen, wo du die Futterstelle in einem Tierheim aufstellen sollst. Es gibt drei Hundehütten und von jeder Hütte sollte die Futterstelle gleich weit entfernt sein. Hier kommt jetzt der Umkreis ins Spiel.
Du bildest ein Dreieck, dass die drei Hundehütten als Ecken hat. Dann konstruierst du zwei Mittelsenkrechten von diesem Dreieck. An dem Punkt, bei dem sich die Mittelsenkrechten schneiden, hast du den Mittelpunkt des Umkreises.
Von dort aus sind alle Ecken und somit alle Hundehütten gleich weit entfernt. Jeder Hund hat dann den gleichen Weg, um zu seinem Napf zu kommen.
Mittelsenkrechte Dreieck — häufigste Fragen
(ausklappen)
Mittelsenkrechte Dreieck — häufigste Fragen
(ausklappen)-
Was ist eine Mittelsenkrechte in einem Dreieck?Eine Mittelsenkrechte in einem Dreieck ist eine Gerade, die senkrecht auf einer Dreiecksseite steht und genau durch deren Mittelpunkt verläuft. Weil ein Dreieck drei Seiten hat, gibt es drei Mittelsenkrechten. Sie werden oft als
 ,
,  und
und  bezeichnet.
bezeichnet.
-
Warum schneiden sich die Mittelsenkrechten im Punkt M?Die Mittelsenkrechten schneiden sich im Punkt M, weil es genau einen Punkt gibt, der von allen drei Eckpunkten A, B und C gleich weit entfernt ist. Dieser gemeinsame Schnittpunkt heißt M. Von M aus lässt sich ein Kreis zeichnen, der durch alle Eckpunkte des Dreiecks geht.
-
Wie konstruiere ich eine Mittelsenkrechte mit Zirkel und Lineal?Eine Mittelsenkrechte konstruierst du, indem du um die beiden Endpunkte einer Seite mit dem Zirkel Kreisbögen mit gleichem Radius zeichnest, der größer als die halbe Seitenlänge ist. Die Bögen schneiden sich in zwei Punkten. Verbinde diese Schnittpunkte mit dem Lineal, dann erhältst du die Mittelsenkrechte.
-
Wann reicht es, nur zwei Mittelsenkrechten zu zeichnen?Es reicht, nur zwei Mittelsenkrechten zu zeichnen, wenn du den Punkt M bestimmen willst. Der Schnittpunkt dieser beiden Mittelsenkrechten ist bereits der gemeinsame Schnittpunkt aller drei. Die dritte Mittelsenkrechte ist dann nur noch zum Überprüfen nötig, weil sie durch denselben Punkt M verlaufen muss.
-
Wie konstruiere ich den Umkreis eines Dreiecks aus dem Punkt M?Den Umkreis eines Dreiecks konstruierst du, indem du die Zirkelspitze in den Punkt M setzt und als Radius den Abstand von M zu einem Eckpunkt nimmst. Zeichnest du damit einen Kreis, liegen alle Eckpunkte auf der Kreislinie. Als Radius geht auch der Abstand zu B oder C.
Winkelhalbierende
Super! Du weißt nun, was eine Mittelsenkrechte ist und wie du sie in einem Dreieck konstruierst. Du willst mehr über Winkelhalbierende erfahren? Dann schau dazu direkt in unser Video rein!