Oberfläche Kegel
Du willst wissen, wie du die Oberfläche eines Kegels berechnen kannst? Hier im Beitrag und in unserem Video erfährst du es!
Inhaltsübersicht
Wie berechnest du die Oberfläche vom Kegel?
Den Kegel kennst du aus dem Alltag in Form von Eiswaffeln, Schultüten oder Turmdächern. Er hat einen Kreis als Grundfläche G und eine Spitze. Die Fläche zwischen Grundfläche und Spitze nennst du Mantelfläche M.
Wenn du diese beiden Flächen addierst, erhältst du die gesamte Oberfläche des Kegels.
Oberfläche O = Grundfläche + Mantelfläche = G + M
Setzt du nun die Formeln für die Grundfläche und die Mantelfläche ein, bekommst du:
O = r2 · π + r · π · s
Die Grundfläche hat einen Radius r. Das ist der Abstand vom Kreismittelpunkt bis zum Rand des Kegels. Die Mantellinie s beschreibt den Abstand von der Kreislinie bis zur Spitze.
Wie berechnest du die Oberfläche eines Kegels Schritt für Schritt?
Um die Oberfläche eines Kegels zu berechnen, musst du die Größe seiner beiden Teilflächen ausrechnen und zusammenzählen.
Um die gesamte Oberfläche zu berechnen, gehst du Schritt für Schritt vor:
- Berechne die Grundfläche G
- Berechne die Mantelfläche M
- Addiere die Flächen G und M
Die Grundfläche des Kegels ist ein Kreis, deshalb berechnest du sie mit der Formel für den Flächeninhalt eines Kreises:
G = r2 · π
Um die Mantelfläche des Kegels zu berechnen, kannst du folgende Formel verwenden:
M = r · π · s
Im letzten Schritt addierst du deine Ergebnisse für G und M nur noch:
O = G + M
Schauen wir uns das mal an einem Beispiel an.
Oberfläche eines Kegels — Beispiel
Wir betrachten zum Berechnen der Oberfläche einen Kegel mit Radius r = 5 cm und Mantellinie s = 12 cm.
1. Grundfläche G berechnen:
G = r2 · π
G = (5 cm)2 · π ≈ 78,5 cm2
2. Mantelfläche M berechnen:
M = r · π · s
M = (5 cm) · π · (12 cm) ≈ 188,5 cm2
3. Flächen addieren:
O = G + M
O = 78,5 cm2 + 188,5 cm2 = 267 cm2
Die Kegeloberfläche ist in diesem Beispiel also O = 267 cm2 groß. Du kannst mit der Formel immer die Fläche beim Kegel berechnen.
Tipp: Alternativ kannst du den Radius und die Mantellinie auch direkt in die Formel O = r2 · π + r · π · s einsetzen.
Wenn in einem Beispiel nur Radius und Höhe des Kegels gegeben sind, musst du die Mantellinie mit dem Satz des Pythagoras
berechnen. Verwende dafür 
.
Oberfläche eines Kegels — Übung
Berechne den Oberflächeninhalt von dem Kegel mit Radius r = 3 cm und Mantellinie s = 8 cm.
Lösung:
O = r2 · π + r · π · s
O = (3 cm)2 · π + (3 cm) · π · (8 cm)
O = 9 cm2 · π + 24 cm2 · π = 33 cm2 · π ≈ 103,7 cm2
Damit hat dieser Kegel einen Flächeninhalt von ungefähr 103,7 cm².
Oberfläche Kegel — häufigste Fragen
-
Wie wird die Mantelfläche eines Kegels berechnet? Die Mantelfläche eines Kegels wird mit der Formel M = r · π · s berechnet, wobei r der Radius der Grundfläche und s die Mantellinie (schräge Seite des Kegels) ist. -
Wie wird die Oberfläche eines Kegels berechnet? Die Oberfläche eines Kegels wird mit der Formel O = r2 · π + r · π · s berechnet. Dabei ist r der Radius der Grundfläche und s die Mantellinie. Es werden Grund- und Mantelfläche addiert. -
Welche Formeln gibt es für die Flächen und das Volumen eines Kegels? Kegel Formeln:
- Oberfläche Kegel: O = r2 · π + r · π · s
- Mantelfläche Kegel: M = r · π · s
-
Volumen Kegel: V =
· r2 · π · h
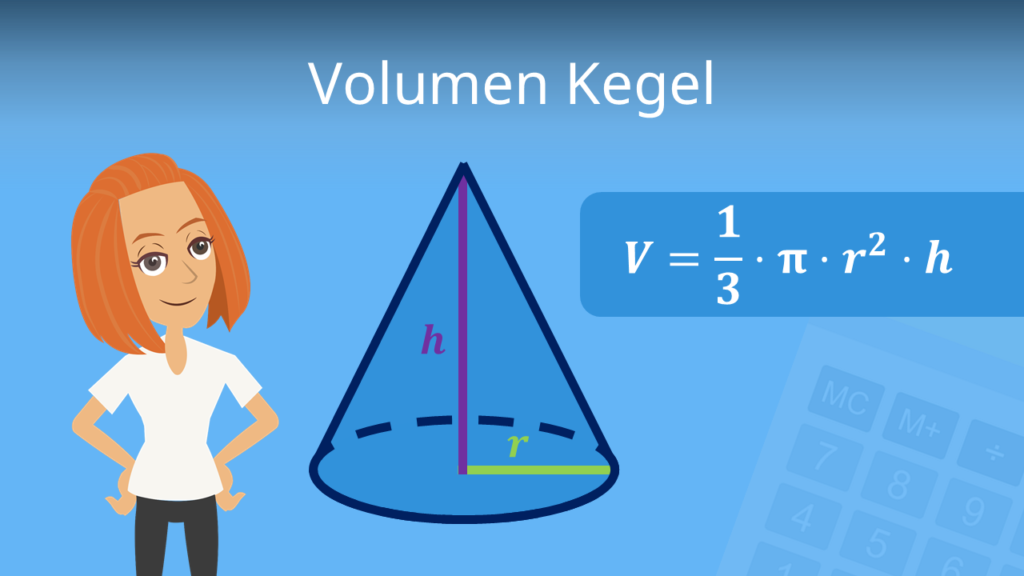
Volumen Kegel
Du möchtest jetzt noch wissen, wie viel in so einen Kegel hinein passt? Dann schau dir hier unser Video zum Volumen eines Kegels an!
